Prizmas tilpums — teorija. Matemātika (Skola2030), 9. klase.

VIDEO KURSS MATEMĀTIKĀ 9. KLASEI

PALĪGSMĀCĪBĀS.LV

Izmantojot prizmas izmērus, var aprēķināt tās tilpumu.

Tilpums rāda, cik daudz vielas var iepildīt dotajā traukā vai arī cik daudz izejmateriāla nepieciešams, lai izgatavotu kādu objektu.

Prizmas tilpums ir vienāds ar tās pamata laukuma un augstuma reizinājumu.

V = S_{pam .} \cdot H

, kur \(H\) - prizmas augstums (taisnas prizmas sānu šķautne).

Tātad, lai aprēķinātu taisnas prizmas tilpumu, nepieciešams aprēķināt (vai zināt) prizmas

pamata daudzstūra laukumu,
augstumu.

Lai noteiktu pamata daudzstūra laukumu, svarīgi noskaidrot, kāda ģeometriskā figūra ir taisnas prizmas pamatā. Taisnas prizmas pamatā var būt jebkurš daudzstūris:

taisnstūris,
kvadrāts,
rombs,
paralelograms,
trapece,
trijstūris, u.c.

Lai varētu aprēķināt tilpumu jebkurai prizmai, atkārto daudzstūru laukuma formulas!

\begin{array}{l} S_{taisnst .} = a \cdot b \\ S_{kvadr .} = a^{2} \\ S_{rombs} = a \cdot h = \frac{d_{1} \cdot d_{2}}{2} \\ S_{paralelograms} = a \cdot h_{a} \\ S_{trapece} = \frac{a + b}{2} \cdot h \\ S_{taisnl . trijst .} = \frac{a \cdot b}{2} \\ S_{trijst .} = \frac{a \cdot h_{a}}{2} \end{array}

Piemērs:

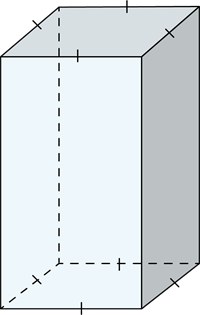
Prizmas pamatā ir kvadrāts, kura mala ir \(5\) \(cm\) gara, bet prizmas augstums ir \(8\) \(cm\).

Aprēķini prizmas tilpumu!

V = S_{pam .} \cdot H

S_{pam .} = a^{2} = 5^{2} = 25 ({cm}^{2})

V = 25 \cdot 8 = 200 ({cm}^{3})

Atbilde: Prizmas tilpums ir \(200\) \(cm^3\).

Piemērs:

Taisnas prizmas pamats ir taisnleņķa trijstūris, kura katetes ir \(4\) \(cm\) un \(8\) \(cm\), bet prizmas augstums ir \(12\) \(cm\).

Aprēķini prizmas tilpumu!

Tā kā prizmas pamats ir taisnleņķa trijstūris, aprēķina tā laukumu

S_{Δ} = \frac{a \cdot b}{2}

, kur \(a\) un \(b\) ir katetes.

S_{Δ} = \frac{4 \cdot 8}{2} = \frac{32}{2} = 16 ({cm}^{2})

V = S_{Δ} \cdot H

, kur \(H\) -augstums

V = 16 \cdot 12 = 192 ({cm}^{3})

Atbilde: Tilpums ir \(192\) \(cm^3\).

Piemērs:

Taisnas prizmas pamatā ir trapece, kuras pamatu garumi ir \(8\) \(cm\) un \(12\) \(cm\), bet trapeces augstums ir \(6\) \(cm\). Prizmas augstums ir \(10\) \(cm\).

Aprēķini prizmas tilpumu!