Ar pirmās pakāpes atvasinājumu nevar iegūt pilnīgu priekšstatu par funkcijas grafika formu atsevišķos definīcijas apgabala intervālos.
Grafiks var būt izliekts (vai arī - izliekts uz augšu) vai ieliekts (izliekts uz leju).
Līniju sauc par izliektu kādā intervālā, ja tā atrodas zem pieskares, kas novilkta brīvi izraudzītā līnijas punktā (attēlā pieskare zaļā krāsā, izliekta līnija \(AB\)).
Līniju sauc par ieliektu kādā punktā, ja tā atrodas virs pieskares, kas novilkta brīvi izraudzītā līnijas punktā (attēlā pieskare sarkanā krāsā, ieliekta līnija \(BC\)).
Lai vieglāk atcerēties, ieliekts - ieleja, izliekts - izceļas.

Ja intervālā \((a;b)\) funkcijai eksistē otrās kārtas atvasinājums un visos intervāla punktos
- , tad grafiks šajā intervālā ir izliekts (uz augšu);
- , tad grafiks ir ieliekts (uz leju).
Par pārliekuma punktu sauc tādu grafika punktu, kurš atdala līknes izliekto daļu no ieliektās daļas.
Jāievēro, ka ne vienmēr punktos, kuros 2. kārtas atvasinājums ir vienāds ar nulli vai neeksistē, funkcijai ir pārliekums. Piemēram, funkcijas otrās kārtas atvasinājums ir nulle, ja \(x=0\), tomēr šajā punktā funkcijas grafikam nav pārliekuma punkta.
Nosakot pārliekuma punktus, jāatrod tās argumenta vērtības, kurām 2. kārtas atvasinājums ir vienāds ar nulli vai neeksistē, un jāpārbauda, vai šajos punktos 2. kārtas atvasinājums maina zīmi.
Funkcijas pārliekuma punktu noteikšanas algoritms
1) Atrod 1. kārtas atvasinājumu.
2) Atrod 2. kārtas atvasinājumu.
3) Atrisina vienādojumu un atrod visas tās \(x\) vērtības, ar kurām neeksistē. Iegūtos skaitļus sakārto augošā secībā.
4) No katra intervāla brīvi izraugās skaitli un ievieto , nosaka 2. atvasinājuma zīmi. Ja blakus intervālos 2. atvasinājuma zīme atšķiras, tad \(x\) ir pārliekuma punkta abscisa.
5) Atrod pārliekuma punkta ordinātu, ievietojot dotajā funkcijā pārliekuma punkta abscisu.
1. uzdevums
Izmantojot 2. atvasinājumu, nosaki, vai funkcijas grafiks ir izliekts vai ieliekts.
Risinājums
Redzam, ka otrais atvasinājums ir pozitīvs, neatkarīgi no argumenta \(x\). Tātad funkcija visā savā definīcijas apgabalā ir ieliekta. Funkcijai nav pārliekuma punkta.
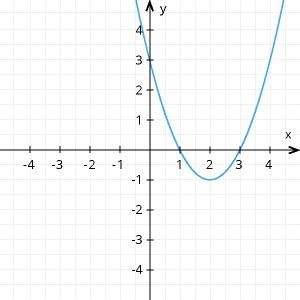
Kā zināms, dotās funkcijas grafiks ir parabola, tās zari ir uz augšu, funkcija ir ieliekta.
2. uzdevums
Nosaki funkcijas grafika pārliekuma punktu abscisas!
1) Nosaka funkcijas 1. kārtas atvasinājumu:
2) Atrod funkcijas 2. kārtas atvasinājumu:
3) Atrisina vienādojumu:
Iegūtos skaitļus sakārto augošā secībā.
\(x\) | −1 | \(0\) | 1 | ||||
\(-\) | \(+\) | \(-\) | \(+\) | ||||
\(f(x)\) | izliekta | p. | ieliekta | p. | izliekta | p. | ieliekta |
Apzīmējums tabulā: p. - ir funkcijas pārliekuma punkts.
No katra intervāla brīvi izraugās skaitli un ievieto . Nosaka 2. atvasinājuma zīmi.
Piemēram, no pirmā intervāla izvēlas skaitli \(x=-10\)
\( \)
Tā kā šajos punktos 2. kārtas atvasinājums maina zīmi, tad var secināt, ka visas 2. kārtas atvasinājuma saknes ir pārliekuma punkti.
Citu pārliekuma punktu nav, jo dotā funkcija definēta visām reālām \(x\) vērtībām.
Atbilde: Pārliekuma punktu abscisas ir .
Atsauce:
Materiālu sagatavoja Mg. math. Laima Baltiņa
Dainis Kriķis. Kārlis Šteiners. Matemātiskās analīzes elementi vidusskolai. 1. daļa. izm. 160.-163. lpp.