Ja funkcija ir definēta intervālā , tad var pētīt funkcijas izturēšanos, argumenta vērtībām neierobežoti palielinoties, t.i., kad . Pieņemsim, ka argumenta vērtībām neierobežoti palielinoties, funkcijas vērtības arvien mazāk atšķiras no skaitļa \(A\), t.i. , ja . Tas nozīmē, ka starpības modulis ir mazāks par jebkuru pozitīvu skaitli , ja vien argumenta \(x\) vērtības ir pietiekami lieli skaitļi. Šādā gadījumā raksta: . Lasa - "funkcijas \(f(x)\) robeža, \(x\) tiecoties uz bezgalību, ir skaitlis \(A\)".
Skaitli A sauc par funkcijas \(f(x)\) robežu, kad , ja katram pozitīvam skaitlim var atrast tādu pozitīvu skaitli , ka ar visām tām \(x\) vērtībām, kas lielākas nekā \(N\), ir spēkā nevienādība .
Lietojot matemātiskās loģikas simbolus, definīciju var pierakstīt saīsināti:
, ka , ir .
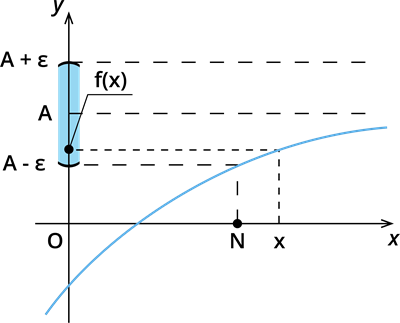
Tas nozīmē, ka jebkurā pēc patikas mazā ap skaitli \(A\) konstruētā intervālā, būs iespējams atrast tik lielu \(x\), ka tā funkcijas vērtība atradīsies šajā intervālā.
Analogi saprot jēdzienu .
Ja funkcija ir definēta intervālā un , tad robežas pieraksta simbola "" priekšā neliek nekādu zīmi, un raksta .
Vidusskolas standartā ir prasība pierādīt robežas eksistenci ar robežas definīciju.
Piemērs:
Lietojot funkcijas robežas definīciju, pierādi, ka
Redzam, ka jebkuram eksistē atbilstošs , kur .
Līdz ar to ir pierādīts, ka
Tātad .
Atsauce:
Materiālu sagatavoja Mg. math. Laima Baltiņa, Jelgavas Tehnoloģiju vidusskolas matemātikas skolotāja