Aplūkosim piemēru, ar kura palīdzību var veidot izpratni par funkcijas robežu.
Dota funkcija
Ko var pateikt par šo funkciju, pirms konstruēts tās grafiks?
Var aprēķināt definīcijas apgabalu.
Tātad dotās funkcijas definīcijas apgabals ir .
Izmantojot kādu no aplikācijām konstruējam funkcijas grafiku.
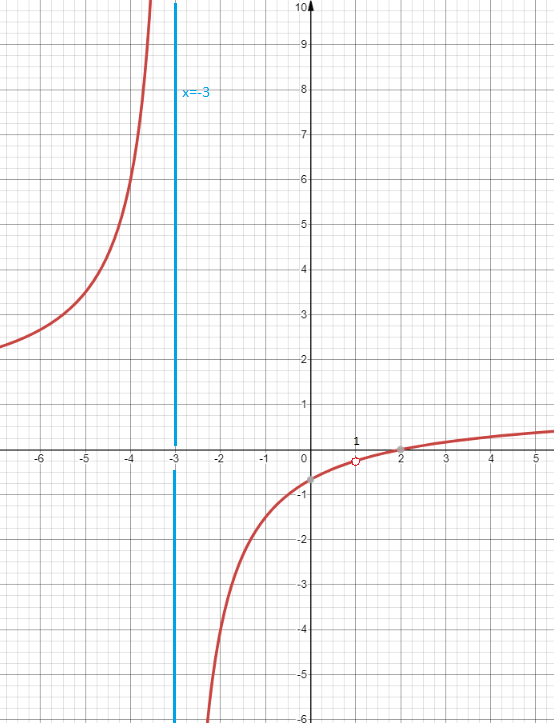
Redzam, kāds ir funkcijas novietojums argumenta \(x=-3\) tuvumā. Skatoties no kreisās puses, funkcijas vērtības kļūst bezgalīgi lielas, bet skatoties no labās puses, funkcijas vērtības kļūst bezgalīgi mazas.
Pieraksts nozīmē robežu, kad arguments \(x\) tiecas uz \(-3\) no kreisās puses.
nozīmē robežu, kad arguments \(x\) tiecas uz \(-3\) no labās puses.
Grafikā var redzēt, ka pie argumenta vērtības \(x=1\), kas arī nepieder definīcijas apgabalam, situācija ir cita.
Funkcijas vērtība, ja \(x\) tiecas uz skaitli \(1\), ir galīgs skaitlis. Bet kā to iegūt, ja funkcijas vērtību pie \(x=1\) nav iespējams aprēķināt?
Izmantojot Excel vai parastu kalkulatoru, var aprēķināt funkcijas vērtības tādām \(x\) vērtībām, kas arvien mazāk atšķiras no skaitļa \(1\).
Piemēram, izvēlas \(x=0,9\), \(x=0,99\), \(x=0,9999\)
Eksperimentāli iegūstam skaitli, kas ir tuvu skaitlim \(-0,25\). Arī šo situāciju var pierakstīt, izmantojot robežas jēdzienu:
Dotajai funkcijai no grafika var nolasīt arī sekojošas robežas:
Tātad \(x\) tuvinot "aizliegtai" vērtībai vai bezgalībai, var iegūt vērtību, kam funkcija tuvojas, bet nesasniedz.
No grafika var nolasīt vai skaitliski var demonstrēt, kā veidojas robeža, bet tas nav pierādījums.
Robežu aprēķināšanu mācīsimies šajā tēmā tālāk.
Līdzīgas situācijas var apskatīt arī nākošā piemērā.
Dots funkcijas grafiks. Kādas robežas ir jēga aplūkot un cik ir to vērtība?
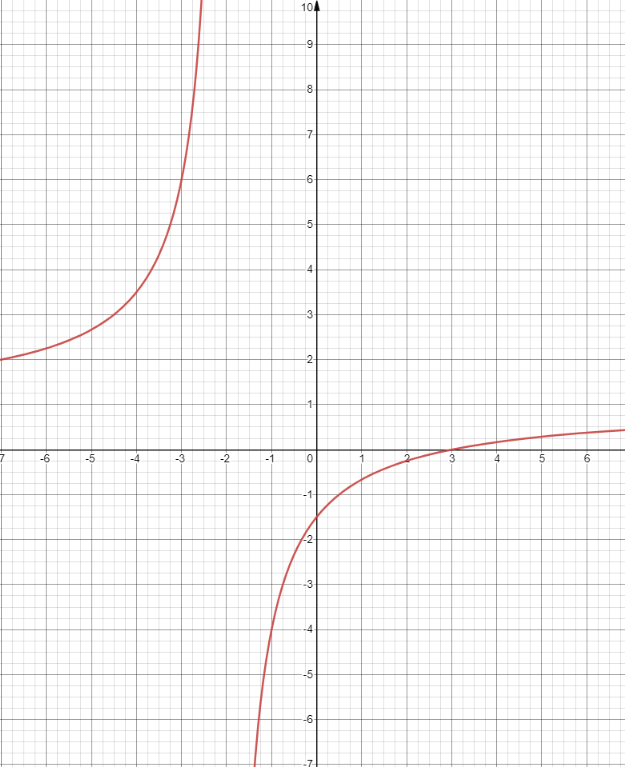
Atsauce:
Idejas autors Toms Akmens, Tukuma Raiņa ģimnāzijas matemātikas un fizikas skolotājs
Materiālu sagatavoja Laima Baltiņa, Mg. math,. Jelgavas Tehnoloģiju vidusskolas matemātikas skolotāja