Tilpums rotācijas ķermenim, kuru ierobežo f(x) un g(x), rotējot ap Ox asi — teorija. Matemātika (Skola2030), Matemātika II.

Video mācību materiāli

"MATEMĀTIKA II"

PALĪGSMĀCĪBĀS.LV

Tilpums rotācijas ķermenim, kuru nosaka divas funkcijas.

Pieņemsim, ka kāda figūra, kuru definē funkcija $f(x)$ un $g(x)$ rotē ap $Ox$ asi.

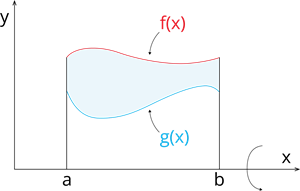
Katrs šo funkciju šķēluma laukuma punkts rotē ap $Ox$ asi un rodas telpiska figūra ar izdobtu vidu.

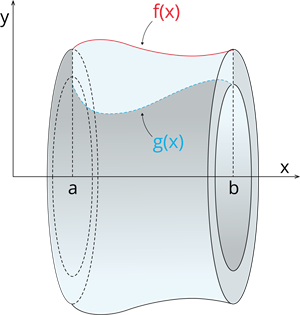
Tilpumu rotācijas ķermenim, kas rodas, rotējot ap $Ox$ asi figūrai, kuru ierobežo līnijas $f(x)$ un $g(x)$, aprēķina kā divu ķermeņu tilpumu starpību.

V = {π \int}_{a}^{b} f^{2} (x) dx - {π \int}_{a}^{b} g^{2} (x) dx = π \int_{a}^{b} (f^{2} (x) - g^{2} (x)) dx

Piemērs:

Aprēķini tilpumu rotācijas ķermenim, kas rodas, rotējot ap Ox asi figūrai, ko ierobežo līnijas

y = x^{2}, y = 2 x

Risinājums.

Skicē grafikus, lai iegūtu figūru, kura rotē ap $Ox$ asi. Abi grafiki krustojas punktos $(0;0)$ un $(2;2)$, šos punktus var nolasīt no grafika vai arī atrisina vienādojumu:

\begin{array}{l} x^{2} = 2 x \\ x^{2} - 2 x = 0 \\ x = 0; x = 2 \end{array}

Ievēro, ka ārējo ķermeņa virsmu nosaka funkcija $y=2x$, bet iekšējo virsmu nosaka

y = x^{2}

Tātad

$\begin{array}{l} V = {π \int}_{0}^{2} (4 x^{2} - x^{4}) dx = \\ = π (\frac{{4 x}^{3}}{3} - \frac{x^{5}}{5})| \begin{array}{l} 2 \\ 0 \end{array} = \\ = π (\frac{32}{3} - \frac{32}{5} - 0) = 32 π (\frac{1}{3} - \frac{1}{5}) = \frac{64 π}{15} \end{array}$

Atbilde: Rotācijas ķermeņa tilpums ir

\frac{64}{15} π

tilpuma vienības.

Atsauce:

Materiālu sagatavoja Mg. math. Laima Baltiņa

Skola2030 kursu materiāli

Iepriekšējā teorija

Atgriezties tēmā

Nākamais uzdevums

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

Video mācību materiāli

"MATEMĀTIKA II"

PALĪGSMĀCĪBĀS.LV

10. Tilpums rotācijas ķermenim, kuru ierobežo f(x) un g(x), rotējot ap Ox asi

Teorija