Kastes maksimalais tilpums. Atvasinājums. — teorija. Matemātika (Skola2030), Matemātika II.

Video mācību materiāli

"MATEMĀTIKA II"

Piemērs:

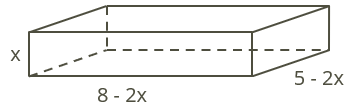
Kartona lapas izmēri ir $8$ $dm$ un $5$ $dm$ . Izgriežot stūros vienādus kvadrātus un apmales atlokot, jāizveido kastīte ar vislielāko tilpumu. Sastādi funkcionālo sakarību $V(x)$, kur $V$ - kastītes tilpums un $x$ - izgriezta kvadrāta malas garums.

Aprēķini kastītes maksimālo tilpumu, izmantojot atvasinājumu!

Risinājums

$x$ ... tik

dm

ir kastes augstums,

$8-2x$ ... tik

dm

ir kastes garums,

$5-2x$ ... tik

dm

ir kastes platums.

Uzraksta tilpumu:

\begin{array}{l} V (x) = (8 - 2 x) (5 - 2 x) \cdot x \\ V (x) = 40 x - 26 x^{2} + 4 x^{3} \end{array}

Nosaka definīcijas apgabalu. Kastes, augstums, garums un platums ir pozitīvi skaitļi:

\begin{array}{l} \{\begin{cases} 8 - 2 x > 0 \\ 5 - 2 x > 0 \\ x > 0 \end{cases} \{\begin{cases} x < 4 \\ x < 2,5 \\ x > 0 \end{cases} \\ x \in (0; 2,5) \end{array}

Atrod funkcijas kritiskos punktus.

1) Atvasina tilpuma funkciju:

\begin{array}{l} V^{'} (x) = {(40 x - 26 x^{2} + 4 x^{3})}^{'} = \\ = 40 - 26 \cdot 2 x + 43 \cdot 3 x^{2} = \\ = 40 - 52 x + 12 x^{2} \end{array}

2) Atvasinājumu pielīdzina nullei:

\begin{array}{l} V^{'} (x) = 0 \\ 40 - 52 x + 12 x^{2} = 0 \\ 12 x^{2} - 52 x + 40 = 0 | : 4 \\ 3 x^{2} - 13 x + 10 = 0 \\ x_{1} = 1; x_{2} = 3 \frac{1}{3} \end{array}

Nosaka ekstrēmus definīcijas apgabalā:

$x$	$(- \infty; 1)$	$(1; 3 \frac{1}{3})$	$(3 \frac{1}{3}; + \infty)$
$V^{'} (x)$	$+$	$-$	$+$
$V(x)$	aug $↗$	dilst $↘$	aug $↗$

Secinām, ka $x=1$ ir maksimuma punkts. Funkcija ir nepārtraukta, tāpēc tai intervālā $(0;2,5)$ ir tikai viens ekstrēma punkts - maksimuma punkts. Tātad funkcijai $V(x)$ šajā punktā ir vislielākā vērtība.

Aprēķinām lielāko vērtību:

$V(1) = 40-26+4=18$ (

{dm}^{3}

)

Atbilde: Funkcionālā sakarība

V (x) = 40 x - 26 x^{2} + 4 x^{3}

, maksimālais tilpums ir $18$

{dm}^{3}

VISC piedāvātie vērtēšanas kritēriji eksāmenā

1 punkts	Iegūst funkcionālo sakarību $V(x).$
1 punkts	Aprēķina funkcijas atvasinājumu.
1 punkts	Nosaka funkcijas kritiskos punktus.
2 punkti	Pamato maksimuma punktu un aprēķina funkcijas maksimālo vērtību.
1 punkts	Izdara secinājumu par $x > 3 \frac{1}{3}$ / nosaka definīcijas apgabalu.

Atsauce:

Materiālu sagatavoja Mg. math. Laima Baltiņa

VISC prezentācija (Aivars Ančupāns) 2022. nov.

Iepriekšējā tēma

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

Video mācību materiāli

"MATEMĀTIKA II"

PALĪGSMĀCĪBĀS.LV

1. Kastes maksimalais tilpums. Atvasinājums.

Teorija