3. Virknes uzdošanas veidi

Skaitļu virknes definīcijas apgabals ir naturālo skaitļu kopa.

 

Skaitļus, kas veido skaitļu virkni sauc par virknes locekļiem un apzīmē ar mazajiem burtiem un indeksiem, piemēram $a_i$, kur \(i\) norāda virknes locekļa kārtas numuru. Pašu virkni apzīmē ar $\left(a_n\right)$.

 

Ja virkne definēta visā naturālu skaitļu kopā $\mathrm{\mathbb{N}}$, tad to sauc par bezgalīgu virkni. Ja virkne definēta naturālu skaitļu kopas galīgā apakškopā, tad saka, ka virkne ir galīga.

 

Lai definētu skaitļu virkni, norāda paņēmienu, ar kuru var atrast jebkuru virknes locekli.

 

 

1) Virkni var uzdot ar vārdiem vai uzrakstot visus virknes locekļus.

Piemēram, skaitļa \(75\) dalītāju virkne: \(1;3;5;15;25;75\). Šī virkne ir galīga.

 

2) Virknes locekļus var sakārtot tabulā.

Ar tabulu parasti uzdod galīgas virknes. Tabulas vienā rindā raksta naturālos skaitļus - virknes locekļu kārtas numurus, bet otrā - atbilstošus reālos skaitļus (virknes locekļu vērtības).

Piemēram, nedēļas darbadienās nostrādātās stundas

 

3) Virkni var uzdot grafiski.

Skaitļu virknes grafiks ir punktu kopa, kas var atrasties tikai I vai IV kvadrantā, jo skaitļu virknes definīcijas apgabals ir naturālo skaitļu kopa. Grafikā katrai naturālai argumenta vērtībai, kas ir virknes locekļu kārtas numuri, atbilst viena funkcijas vērtība - attiecīgais virknes loceklis.

No attēlā dotā grafika varam nolasīt, ka

 

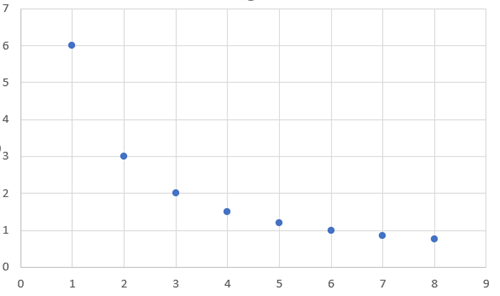
Ievēro! Skaitļu virknes grafiks ir diskrēta kopa, t.i., virknes grafiks nav nepārtraukta līnija.

 

4) Virkni var uzdot ar analītisku izteiksmi jeb formulu, pēc kuras katrai argumenta \(n\) vērtībai var noteikt atbilstošo virknes locekli. Šo izteiksmi sauc par virknes vispārīgā locekļa formulu.

Piemēram, zinot virknes $\left(z_n\right)$ vispārīgā locekļa formulu $z_n=-3n+2$, var aprēķināt jebkuru no virknes locekļiem:

 

5) Virkni var definēt rekurenti, t.i., norādot pirmo vai dažus pirmos virknes locekļus un to, kā, izmantojot iepriekšējo locekli/locekļus, var iegūt nākamo virknes locekli.

Piemēram, ar rekurences formulu

 $\begin{array}{l}{f}_1=f_2=1\\ f_{n+1}=f_{n-1}+f_n\end{array}$

ir uzdota *Fibonači virkne \(1;1;2;3;5;8;... \)  Katrs nākamais virknes loceklis ir divu iepriekšējo virknes locekļu summa.

 

Ar rekurences formulu ir grūti noteikt virknes locekļus ar lielu kārtas numuru. Piemēram, mēs nevaram galvā aprēķināt, cik ir Fibonači virknes tūkstošais loceklis $f_{1000}$, jo tad mums vispirms jāzina, cik ir 999. un 998. virknes loceklis.

 

Matemātikā parasti cenšas noteikt virknes analītisko izteiksmi, uzdodot vispārīgā locekļa formulu.

 

*Itāļu matemātiķis Leonardo Fibonači (ap 1175- ap 1250)