Elipse un tās vienādojums — teorija. Matemātika, Augstskola: 1. kurss.

Elipse un tās vienādojums

Elipsi veido punkti, kuriem attālumu summa no diviem dotiem punktiem, kurus sauc par fokusiem, ir konstanta.

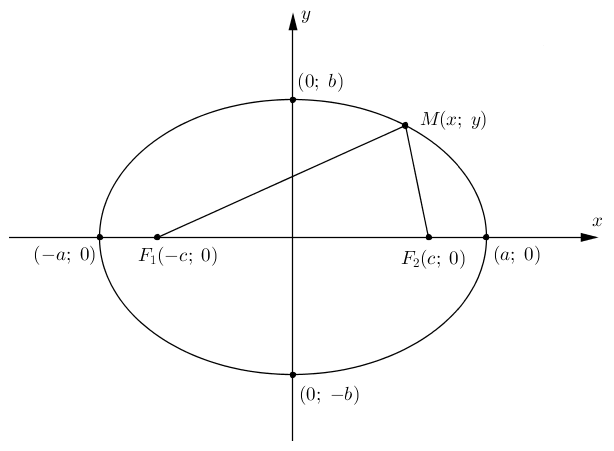
Ja attālumu starp fokusiem apzīmē ar

2 c

un konstanto attālumu summu ar

2 a

, turklāt fokusus novieto uz Ox ass tā, kā tas parādīts zīmējumā, tad ir spēkā sakarība

M F_{1} + M F_{2} = 2 a

jeb

\sqrt{{(x - (- c))}^{2} + {(y - 0)}^{2}} + \sqrt{{(x - c)}^{2} + {(y - 0)}^{2}} = 2 a

No šī vienādojuma var iegūt elipses kanonisko vienādojumu:

\begin{array}{l} \sqrt{{(x + c)}^{2} + y^{2}} + \sqrt{{(x - c)}^{2} + y^{2}} = 2 a \\ \sqrt{{(x + c)}^{2} + y^{2}} = 2 a - \sqrt{{(x - c)}^{2} + y^{2}} \\ {(x + c)}^{2} + y^{2} = 4 a^{2} + {(x - c)}^{2} + y^{2} - 4 a \sqrt{{(x - c)}^{2} + y^{2}} \\ 4 a \sqrt{{(x - c)}^{2} + y^{2}} = 4 a^{2} - 4 cx \\ a \sqrt{{(x - c)}^{2} + y^{2}} = a^{2} - cx \\ a^{2} x^{2} - 2 a^{2} cx + a^{2} c^{2} + a^{2} y^{2} = a^{4} - 2 a^{2} cx + c^{2} x^{2} \\ (a^{2} - c^{2}) x^{2} + a^{2} y^{2} = a^{2} (a^{2} - c^{2}) \\ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - c^{2}} = 1 \\ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{array}

Te tika izmantots tas, ka

b = \sqrt{a^{2} - c^{2}}

jeb

b^{2} = a^{2} - c^{2}

. (Skatīt zīmējumu.)

Vienādojumu

\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1

sauc par elipses kanonisko vienādojumu.

Elipses simetrijas asis sauc par tā asīm un puses no šīm asīm sauc par pusasīm (kanoniskajā vienādojumā a ir garums pusasij, kas atrodas uz Ox ass, b - garums pusasij uz Oy ass).
Elipses simetrijas centru (asu krustpunktu) sauc par elipses centru. Punktus, kuros elipse krusto asis, sauc par elipses virsotnēm.

Iepriekšējā tēma

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

1. Elipse un tās vienādojums

Teorija