Taisnes kanoniskais vienādojums — teorija. Matemātika, Augstskola: 1. kurss.

Katru nenulles vektoru

\vec{a}

, kas ir paralēls taisnei

l

, sauc par šīs taisnes virziena vektoru.

Pieņemsim, ka punkts

M_{0} (x_{0}; y_{0})

ir fiksēts taisnes

l

punkts, bet punkts

M (x; y)

ir jebkurš cits šīs taisnes punkts. Tad vektori

\vec{a} = (a_{x}; a_{y})

\vec{M_{0} M} = (x - x_{0}; y - y_{0})

ir kolineāri.

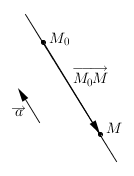
Tas nozīmē, ka šo vektoru koordinātas ir proporcionālas un

\frac{x - x_{0}}{a_{x}} = \frac{y - y_{0}}{a_{y}}

(šeit

\frac{0}{0}

var pieņemt jebkuru vērtību).

Vienādojumu

\frac{x - x_{0}}{a_{x}} = \frac{y - y_{0}}{a_{y}}

sauc par taisnes kanonisko vienādojumu.

Tātad, ja ir zināms kāds taisnes virziena vektors un viens tās punkts, tad var viegli uzrakstīt taisnes vienādojumu.

Tāpēc var viegli aprēķināt vienādojumu taisnei, kas iet caur diviem punktiem

M_{1} (x_{1}; y_{1})

M_{2} (x_{2}; y_{2})

. Kā virziena vektoru var ņemt šo punktu veidoto vektoru

M_{2} M_{1} = (x_{2} - x_{1}; y_{2} - y_{1})

Svarīgi!

Ja taisne iet caur diviem punktiem

M_{1} (x_{1}; y_{1})

M_{2} (x_{2}; y_{2})

, tad tās vienādojums (kanoniskā formā) ir

\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{y - y_{1}}{y_{2} - y_{1}}

Atradi kļūdu?

5. Taisnes kanoniskais vienādojums