Ja telpas bāzei vai plaknes bāzei klāt pievieno arī fiksētu sākuma punktu (koordinātu sākumpunktu), tad iegūst afīnu koordinātu sistēmu.
Tajā katru punktu var viennozīmīgi aprakstīt ar atbilstošā vektora koordinātām attiecīgajā bāzē. Vektoru sauc par punkta rādiusvektoru.
Piemēram, ja dota telpas bāze un vektora koordinātas šai bāzē ir (jeb ), tad saka, ka tādas ir arī punkta koordinātas, un to pieraksta šādi: .
Katram plaknes punktam ir divas koordinātas. Un katram telpas punktam - trīs koordinātas.
Svarīgi!
To, ka punkta un tā rādiusvektora koordinātas ir vienādas, izmanto ļoti daudzu uzdevumu risināšanā. No punktu koordinātām var iegūt to rādiusvektoru koordinātas - un otrādāk.
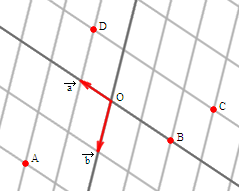
Piemērs:
Šeit koordinātu sākumpunkts ir un bāze ir .
Tādā gadījumā un tātad . Tāpat iegūst, ka , , un, protams, .
Svarīgi!
Ja par bāzi ņem savstarpēji perpendikulārus vektorus ar garumu un fiksē sākuma punktu , tad iegūst speciālu afīnas koordinātu sistēmas gadījumu - Dekarta taisnleņķa koordinātu sistēmu.
Ja tā ir plaknē, tad bāzes vektorus apzīmē ar . Ja telpā - tad attiecīgi .