Vienādojumus \(tgx=a\) un \(ctgx=a\) ērti atrisināt, izmantojot vienības riņķa līniju. Trigonometriskais vienības riņķis ir dots matemātikas eksāmena formulu lapā.
Atrisināsim vienādojumu \(tgx=1\)
Vienības riņķī uz tangensu ass atliek vērtību \(1\).
Uz vienības riņķa līnijas ir divi punkti, kuriem pagrieziena leņķu tangensu vērtība ir \(1\).
Tie ir jeb . Tomēr abus leņķus neraksta atbildē.
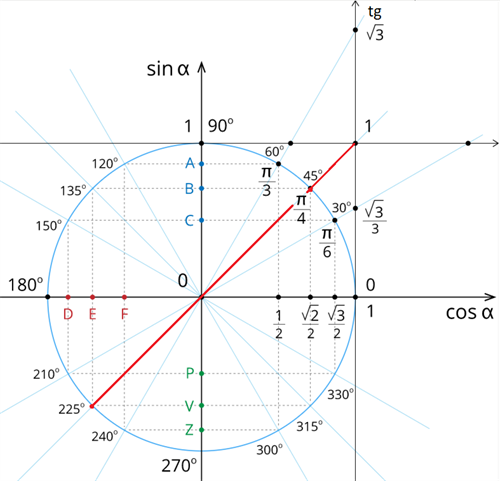
Tā kā abas vērtības savstarpēji atšķiras par tangensa funkcijas periodu , tad abas atbildes var apvienot.
Līdzīgi risina arī kotangensa pamatvienādojumu.
Atrisināsim vienādojumu
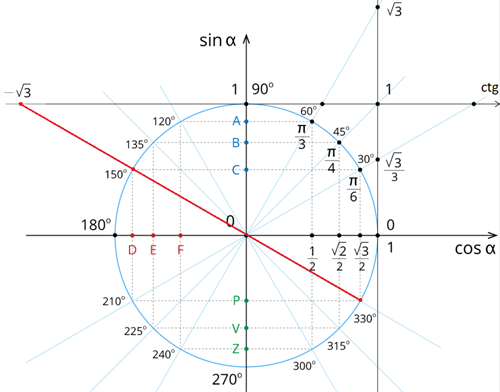
Piemērs:
Ievēro, kā pieraksta tangensa atbildi, ja leņķis ir 4. kvadrantā. Ņem vērā, ka pagrieziena leņķim jābūt no intervāla .
Izpēti tabulu!
Trigonometrisko funkciju salīdzinājums
Funkcija | Vērtību apgabals (\(a\) vērtības) | Definīcijas apgabals (pieļaujamās leņķa \(x\) vērtības) |
\(\sin x\), \(\cos x\) | \([-1;1]\) | |
\(\operatorname{tg}x\) | \(x\neq \frac{\pi}{2}+\pi n\) jeb , kur \(n\in\mathbb{Z}\) | |
\(\operatorname{ctg}x\) | \(x\neq \pi n\) jeb , kur \(n\in\mathbb{Z}\) |