Progresijas — teorija. Matemātika, 12. klase.

Virkni, kurā katru nākamo locekli iegūst, ja iepriekšējam pieskaita vienu un to pašu skaitli (diferenci \(d\)), sauc par aritmētisko progresiju.

Aritmētiskās progresijas vispārīgā locekļa formula ir

a_{n} = a_{1} + (n - 1) \cdot d

Ja izvēlas trīs citu citam sekojošus trīs locekļus, ir spēkā īpašība:

a_{n} = \frac{a_{n - 1} + a_{n + 1}}{2}

Piemēram: ja dota aritmētiskā progresija

2, 6, 10, 14, 18, ...

, redzam, ka

6 = \frac{2 + 10}{2}

14 = \frac{10 + 18}{2}

utt.

Aritmētiskās progresijas pirmo

n

locekļu summa ir

S_{n} = \frac{(a_{1} + a_{n}) \cdot n}{2}

jeb

\begin{array}{l} S_{n} = \frac{a_{1} + a_{1} + (n - 1) \cdot d}{2} \cdot n \\ S_{n} = \frac{2 a_{1} + (n - 1) d}{2} \cdot n \end{array}

Virkni, kurā katru nākamo locekli iegūst, iepriekšējo locekli sareizinot ar vienu un to pašu skaitli (kvocientu

q

), sauc par ģeometrisko progresiju.

Ģeometriskās progresijas vispārīgā locekļa formula ir

b_{n} = b_{1} q^{n - 1}

Ja izvēlas trīs citu citam sekojošus locekļus, ir spēkā īpašība:

b_{n}^{2} = b_{n - 1} \cdot b_{n + 1}

Piemērs:

Ja dota ģeometriskā progresija

3, 6, 12, 24, 48, ...

, tad viegli pārbaudīt, ka

6^{2} = 3 \cdot 12

12^{2} = 6 \cdot 24

, utt.

Ģeometriskās progresijas pirmo

n

locekļu summa ir

S_{n} = \frac{b_{1} (1 - q^{n})}{1 - q}

jeb

S_{n} = \frac{b_{1} - q b_{n}}{1 - q}

Skolas kursā reti lieto šo formulu, bieži vien ir vienkāršāk izrēķināt katru locekli atsevišķi un tos saskaitīt.

Svarīgi zināt un lietot bezgalīgi dilstošas ģeometriskās progresijas summas formulu.

Ģeometrisko progresiju sauc par bezgalīgi dilstošu, ja tās kvocients

q

pēc moduļa ir mazāks par 1 (

|q| < 1

Tātad kvocients var būt gan negatīvs, gan pozitīvs lielums.

Piemēram, kvocients var būt

- 0,3; \frac{1}{\sqrt{2}}; - \frac{1}{3}; \frac{7}{8}

Par bezgalīgi dilstošas ģeometriskās progresijas locekļu summu sauc skaitli, uz kuru tiecas šīs progresijas pirmo

n

locekļu summa,

n

vērtībai neierobežoti palielinoties.

S_{\infty} = \frac{b_{1}}{1 - q}

Piemērs:

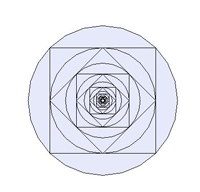
Riņķa līnijā, kuras rādiuss ir 10 cm, ievilkts kvadrāts, kvadrātā ievilkta riņķa līnija utt. - bezgalīgi daudz kvadrātu un riņķa līniju (skat. zīm.). Aprēķini visu kvadrātu perimetru summu.

Risinājums:

Pārbaudīsim, vai kvadrātu perimetri veido bezgalīgi dilstošu ģeometrisko progresiju.

Viegli aprēķināt: ja riņķa līnijas rādiuss ir 10 cm, tad ievilktā kvadrāta mala ir

10 \sqrt{2}

cm, nākošā kvadrāta mala ir 10 cm, nākošā

5 \sqrt{2}

cm utt.

Kvadrātu perimetri veido virkni

40 \sqrt{2}; 40; 20 \sqrt{2}; ...

, kuras kvocients ir

q = \frac{\sqrt{2}}{2}

\begin{array}{l} \frac{b_{2}}{b_{1}} = \frac{40}{40 \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} \\ \frac{b_{2}}{b_{3}} = \frac{20 \sqrt{2}}{40} = \frac{\sqrt{2}}{2} \end{array}

utt.

Redzams, ka

|q| = \frac{\sqrt{2}}{2} < 1

Izmanto bezgalīgi dilstošas ģeometriskās progresijas summas formulu:

S_{\infty} = \frac{b_{1}}{1 - q} = \frac{40 \sqrt{2}}{1 - \frac{\sqrt{2}}{2}} = \frac{40 \sqrt{2}}{\frac{2 - \sqrt{2}}{2}} = \frac{80 \sqrt{2}}{2 - \sqrt{2}}

Iegūto izteiksmi vienkāršo tālāk, atbrīvojoties no iracionalitātes saucējā:

S_{\infty} = \frac{80 \sqrt{2}}{2 - \sqrt{2}} = \frac{80 \sqrt{2} (2 + \sqrt{2})}{(2 - \sqrt{2}) (2 + \sqrt{2})} = \frac{160 \sqrt{2} + 160}{4 - 2} = 80 \sqrt{2} + 80

Atbilde: visu kvadrātu perimetru summa ir

80 \sqrt{2} + 80

Piemērs:

Pārveido skaitli

0, (17)

par parastu daļu!

Risinājums:

Jebkuru skaitli var uzrakstīt kā summu.

0, (17) = 0,1717171717 ... = 0,17 + 0,0017 + 0,000017 + ...

Summas saskaitāmie veido bezgalīgi dilstošu ģeometrisko progresiju, kurā

q = 0,01

, bet pirmais loceklis ir

0, (17)

Izmanto summas formulu:

S_{\infty} = \frac{b_{1}}{1 - q} = \frac{0, 17}{1 - 0, 01} = \frac{0, 17}{0, 99} = \frac{17}{99}

Atbilde:

0, (17) = \frac{17}{99}

Iepriekšējā teorija

Atgriezties tēmā

Nākamais uzdevums

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

7. Progresijas

Teorija