Pitagora teorēmu un trigonometriskās sakarības var lietot tikai taisnleņķa trijstūra elementu aprēķināšanai un tad pietiek ar diviem dotiem lielumiem (divām malām vai leņķi un malu).
Patvaļīga trijstūra aprēķināšanai nepieciešami vismaz trīs doti lielumi. Lieto kosinusu vai sinusu teorēmu.
Kosinusa teorēma. Trijstūra jebkuras malas kvadrāts ir vienāds ar abu pārējo malu kvadrātu summu, no kuras atņemts šo malu reizinājums ar ietvertā leņķa kosinusu: (skatīt zīmējumu).
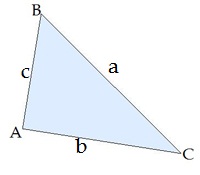
Kosinusu teorēmu parasti lieto, lai aprēķinātu:
- trešās malas garumu, ja dotas divas malas un leņķis starp tām;
- trijstūra leņķa lielumu, ja doti visu trīs malu garumi.
Tā kā viens no trijstūra leņķiem var būt arī plats, jāprot iegūt kosinusa vērtības platiem leņķiem ar redukcijas formulu palīdzību.
Atceries:
Piemērs:
Trijstūra malu garumi ir 4 cm, 6 cm, 8 cm. Aprēķini lielākā leņķa kosinusu!
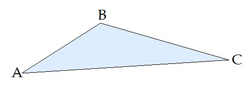
Risinājums: Lielākais leņķis atrodas pretim garākajai malai, tāpēc raksta kosinusu teorēmu garākai malai.
Tā kā kosinuss ir negatīvs platiem leņķiem, var secināt, ka dotais trijstūris ir platleņķa.