Risinot uzdevumus, ļoti svarīgi ir prast iezīmēt leņķus, ko prizmas diagonāles veido ar pamatu un ar sānu skaldnēm.
Leņķis starp slīpni un plakni ir leņķis starp slīpni un tās projekciju plaknē.
Svarīgi!
Lai atrastu slīpnes projekciju plaknē:
1) velk slīpni;
2) no slīpnes galapunkta velk perpendikulu pret plakni;
3) novelk slīpnes projekciju;
4) atzīmē leņķi starp slīpni un tās projekciju.
1) velk slīpni;
2) no slīpnes galapunkta velk perpendikulu pret plakni;
3) novelk slīpnes projekciju;
4) atzīmē leņķi starp slīpni un tās projekciju.
Taisna paralēlskaldņa diagonāles leņķis ar pamata plakni
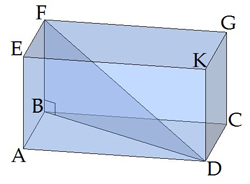
Leņķis ir paralēlskaldņa diagonāles veidotais leņķis ar pamata plakni .
Trijstūris ir taisnleņķa trijstūris.
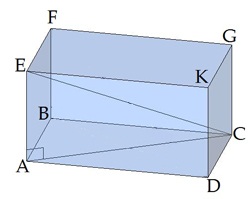
Leņķis ir paralēlskaldņa diagonāles veidotais leņķis ar pamata plakni .
Trijstūris ir taisnleņķa trijstūris.
Taisnstūra paralēlskaldņa diagonāles leņķis ar sānu skaldnēm.
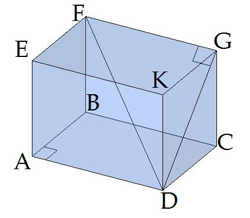
Leņķis ir taisnstūra paralēlskaldņa diagonāles veidotais leņķis ar sānu skaldni .
Ievēro: taisnstūra paralēlskaldņa šķautne ir perpendikulāra pret sānu skaldni, tāpēc trijstūris ir taisnleņķa trijstūris.
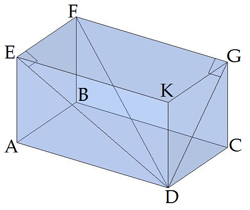

Leņķis ir paralēlskaldņa diagonāles veidotais leņķis ar sānu skaldni .
Ievēro: taisnstūra paralēlskaldņa šķautne ir perpendikulāra pret sānu skaldni, tāpēc trijstūris ir taisnleņķa trijstūris.
Regulāras sešstūra prizmas diagonāles veidotais leņķis ar pamata plakni
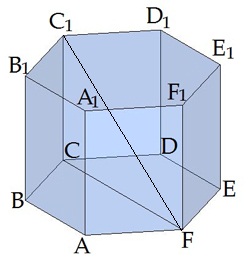
Leņķis ir garākās diagonāles veidotais leņķis ar pamata plakni .
Trijstūris ir taisnleņķa trijstūris.