Pitagora teorēmu un trigonometriskās sakarības var lietot tikai taisnleņķa trijstūra elementu aprēķināšanai.
Patvaļīga trijstūra aprēķināšanai nepieciešami vismaz trīs doti lielumi. Lieto kosinusu vai sinusu teorēmu.
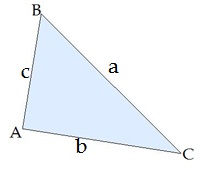
Sinusu teorēma:
Trijstūru malas ir proporcionālas to pretleņķu sinusiem.
Sinusu teorēmu parasti lieto, lai aprēķinātu:
- nezināmos trijstūra malu garumus, ja doti divi leņķi un viena mala;
- trijstūra nezināmo leņķu lielumus, ja doti divu malu garumi un viens pieleņķis.
Tā kā viens no trijstūra leņķiem var būt arī plats, jāprot iegūt sin vērtības platiem leņķiem ar redukcijas formulu palīdzību.
Atceries:
Piemērs:
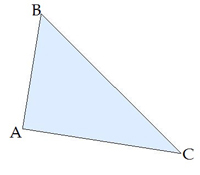
Aprēķini trijstūra malu , ja , un
Risinājums:
Ar sinusu teorēmu var aprēķināt arī apvilktas riņķa līnijas rādiusu
, kur - trijstūrim apvilktās riņķa līnijas rādiuss.
Piemērs:
Aprēķini ap trijstūri apvilktās riņķa līnijas rādiusu, ja viens no tā leņķiem ir , bet šī leņķa pretmala ir .
Risinājums: