Ar riņķa līniju saistītie nogriežņi un taisnes un leņķi
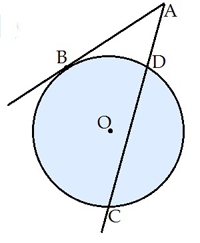
Taisni, kurai ar riņķa līniju ir divi kopīgi punkti, sauc par riņķa līnijas sekanti
(zīm. taisne ).
Nogriezni, kas savieno divus riņķa līnijas punktus, sauc par hordu
(zīm. nogrieznis ).
Taisni, kurai ar riņķa līniju ir tikai viens kopējs punkts, sauc par pieskari
(zīm. taisne ).
Centra leņķis un ievilkts leņķis
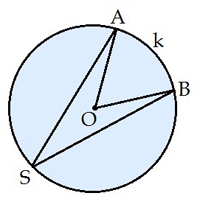
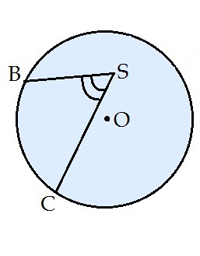
Leņķi, kura virsotne atrodas riņķa centrā, sauc par centra leņķi (zīm. ).
Centra leņķa lielums ir vienāds ar tam atbilstošā loka leņķisko lielumu (zīm. ).
Leņķi, kura virsotne atrodas uz riņķa līnijas, bet malas krusto riņķa līniju, sauc par riņķa līnijā ievilktu leņķi (zīm. ).
Ievilktā leņķa lielums ir vienāds ar pusi no tā loka leņķiskā lieluma, uz kura tas balstās (zīm. ).
Hordas - pieskares leņķis
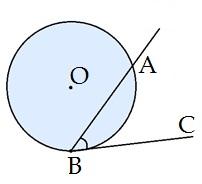
Leņķi, kura virsotne atrodas uz riņķa līnijas un kuram viena mala satur hordu, bet otra mala atrodas uz pieskares, sauc par hordas - pieskares leņķi.
(zīm. ).
Hordas - pieskares leņķis ir vienāds ar pusi no tā loka leņķiskā lieluma, kuru ietver leņķa malas (zīm. ).
Ārējais leņķis
Leņķi, kura virsotne atrodas ārpus riņķa un tā malas krusto riņķa līniju vai arī viena vai abas malas pieskaras riņķa līnijai, sauc par šīs riņķa līnijas ārējo leņķi.
Ārējā leņķa lielums ir vienāds ar pusi no to divu loku leņķisko lielumu starpības, kuri atrodas starp leņķa malām.
Ārējais leņķis var būt dots trīs dažādos veidos.
- Ārējo leņķi var veidot divas pieskares.
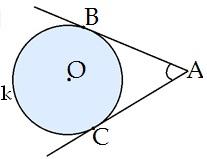
- Ārējo leņķi var veidot viena sekante un pieskare.
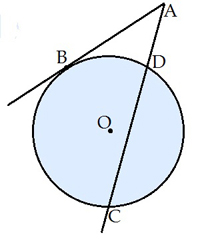
- Ārējo leņķi var veidot divas sekantes.
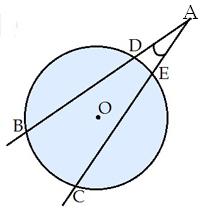
Iekšējais leņķis jeb leņķis starp divām hordām
Leņķi, kura virsotne atrodas riņķa iekšpusē, bet malas krusto riņķa līniju, sauc par iekšēju leņķi (zīm. ).
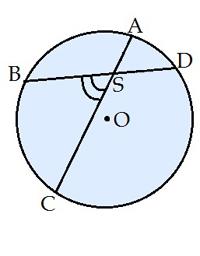
Caur virsotni pagarinot šī leņķa malas, var iegūt divas hordas.
Iekšēja leņķa lielums jeb leņķa lielums starp divām hordām, ir vienāds ar pusi no to divu loku leņķisko lielumu summas, no kuriem viens ir starp leņķa malām, bet otrs ir starp leņķa malu pagarinājumiem (zīm. ).
Skat. atbilstošās formulas matemātikas eksāmena formulu lapā: formulas