Matemātikā ir divi dažādi jēdzieni:
- vektora ģeometriskā projekcija, kas ir vektors;
- vektora projekcija, kas ir skaitlis.
Vektora ģeometriskā projekcija ir vektors, kuru iegūst, no vektora galapunktiem pret izvēlētu asi velkot perpendikulus.
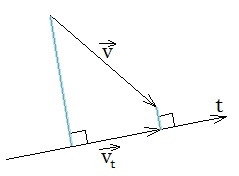
Vektora ģeometriskā projekcija ir vektors .
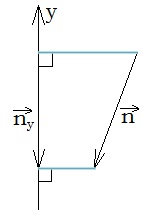
Vektora ģeometriskā projekcija ir vektors .
Vektora projekcija uz ass ir skaitlis, kurš
- vienāds ar vektora ģeometriskās projekcijas garumu, ja ģeometriskās projekcijas un ass vērsumi sakrīt;
- ir pretējs skaitlis ģeometriskās projekcijas garumam, ja ģeometriskās projekcijas un ass vērsumi ir pretēji.
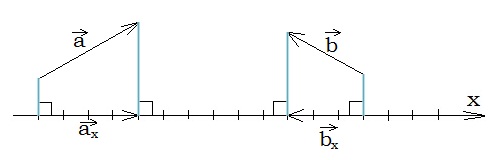
Šeit un .
Ja vektora garums ir un ir vektora un ass veidotais šaurais leņķis, tad vektora projekcijas moduli aprēķina pēc formulas: .
Vektora projekcijas zīmi izvēlas atkarībā no ass virziena.
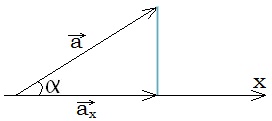
Zīmējumā var redzēt, ka šo formulu var iegūt no sakarības taisnleņķa trijstūrī: