Funkcijas un argumenta pieaugums — teorija. Matemātika, 12. klase.

Video mācību materiāli

"MATEMĀTIKA II"

Starpību starp divām argumenta vērtībām

x_{0}

x_{1}

sauc par argumenta pieaugumu un apzīmē ar simbolu

Δ x

, kur

Δ x = x_{1} - x_{0}

Starpību starp divām funkcijas vērtībām

f (x_{0})

f (x_{1})

sauc par funkcijas pieaugumu un apzīmē ar simbolu

Δ f (x)

, kur

Δ f (x) = f (x_{1}) - f (x_{0})

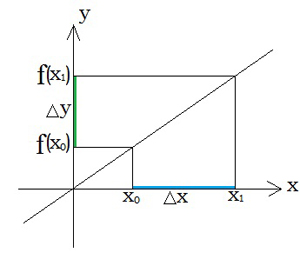
12. klasē jāprot, izmantojot funkcijas un argumenta pieaugumus, dotai taisnei noteikt virziena koeficientu un sekojoši arī taisnei atbilstošo analītisko izteiksmi (formulu).

Kā zināms, lineāras funkcijas virziena koeficients $k = \frac{Δ f (x)}{Δ x}$ .

Piemērs:

Nosaki zīmējumā dotās lineārās funkcijas analītisko izteiksmi!

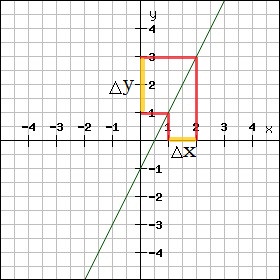
Risinājums:

Lineāras funkcijas vispārīgais veids ir

y = kx + b

Atrodam

k

Ox

ass brīvi izvēlamies

x_{0} = 1

x_{1} = 2

, iegūstam

Δ x = 1

(viena vienība).

Atrodam atbilstošos

f (x_{0}) = 1

f (x_{1}) = 3

, iegūstam

Δ f (x) = 3 - 1 = 2 k = \frac{Δ f (x)}{Δ x} = \frac{2}{1} = 2

Skaitlis

b

ir krustpunkts ar

Oy

asi, redzam, ka

b = - 1

Atbilde: koordinātu plaknē ir attēlota taisne

y = 2 x - 1

Atceries: taisnes virziena koeficients ir vienāds ar taisnes un

Ox

ass veidotā leņķa tangensu:

k = tg α

Piemērs:

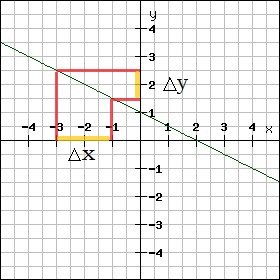
Pēc dotā grafika nosaki dotās taisnes un

Ox

ass veidotā leņķa tangensu.

Risinājums:

Brīvi izvēlas

x_{0} = - 3

x_{1} = - 1

, redzams, ka

f (x_{0}) = 2 \frac{1}{2}

f (x_{1}) = 1 \frac{1}{2}

k = tg α

, tātad

tg α = \frac{Δ f (x)}{Δ x} = - \frac{1}{2}

Atbilde: dotās taisnes un

Ox

ass veidotā leņķa tangenss ir

- \frac{1}{2}

Iepriekšējā teorija

Atgriezties tēmā

Nākamā teorija

Nosūtīt atsauksmi

Atradi kļūdu?

Sūti mums ziņu!

Video mācību materiāli

"MATEMĀTIKA II"

PALĪGSMĀCĪBĀS.LV

4. Funkcijas un argumenta pieaugums

Teorija