OTRĀ SEMESTRA NOSLĒGUMA TESTI
Vienādsānu trijstūra mediāna, kas novilkta pret pamatu, ir arī šī trijstūra augstums un bisektrise.
Vienādsānu trijstūrī leņķi pie pamata ir vienādi.
Vienādsānu trijstūrī leņķi pie pamata ir vienādi.
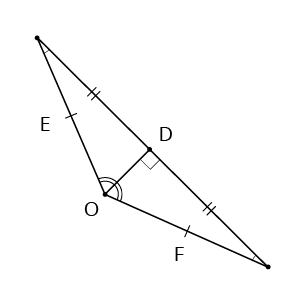
Trijstūris \(EOF\) - vienādsānu trijstūris, un \(OE = OF\) ir tā sānu malas.
\(OD\) jeb mediāna sadala pamatu uz pusēm: \(DE=DF\)
\(OD\) jeb bisektrise dala virsotnes leņķi uz pusēm:
\(OD\) jeb bisektrise dala virsotnes leņķi uz pusēm:
\(OD\) - augstums ir perpendikulārs pamatam:
, tas ir,
Leņķi pie pamata jeb pamata pieleņķi ir vienādi:
Piemērs:
- vienādsānu trijstūris
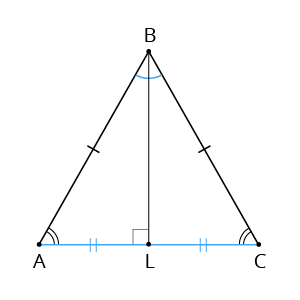
Secinājumi:
\(BL\) - mediāna, tātad \(AL=LC\)
\(BL\) - bisektrise, tātad
\(BL\) - augstums, tātad , tas ir,
Pamata pieleņķi vienādi, tātad
Pamata pieleņķi vienādi, tātad