PIRMĀ SEMESTRA NOSLĒGUMA TESTI
Tu jau pazīsti un proti izmantot garuma mērvienības. Un zini, ka

Un Tu zini, ka figūru laukumu var noteikt, piemēram, saskaitot rūtiņas. Tad laukuma vienība ir rūtiņa.
Virtuves grīdas laukumu vari iegūt, saskaitot grīdas flīzes. Tad laukuma vienība ir flīze.
Ikdienā visbiežāk izmanto laukuma vienības, kuras ir saistītas ar jau pazīstamām garuma vienībām.
Laukuma vienība \(1\) (\(1\) ; \(1\) ) ir kvadrāts, kura malas garums ir \(1 m\) (\(1 dm, 1 m\)).
\(-\) kvadrātmilimetrs
\(-\) kvadrātcentimetrs
\(-\) kvadrātdecimetrs
\(-\) kvadrātmetrs
\(a\) \(-\) ārs
\(ha\) \(-\) hektārs
\(-\) kvadrātkilometrs
Attēlā vari aplūkot, kā veidojas kvadrātmetrs, tajā \(100\) reizes mazāks ir kvadrātdecimetrs, un par kvadrātdecimetru \(100\) reizes mazāks ir kvadrātcentimetrs.
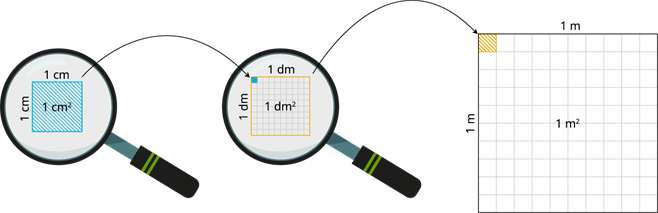
Laukuma vienības viegli atcerēties, ja zini garuma vienības.
Izpēti attēlus! Ievēro, kādi ir katra kvadrāta malu garumi, kā veidojas katra laukuma mērvienība!


Laukuma mērvienību sakarības vari arī izpētīt, uzzīmējot uz rūtiņu lapas kvadrātdecimetru un sadalot to kvadrātcentimetros. Izpēti attēlu!

Katra rūtiņa ir \(1\) . Katrā rindā tādi ir \(10\) .
Un visā kvadrātā ir \(10\) tādas rindiņas.
Un visā kvadrātā ir \(10\) tādas rindiņas.
Tātad \(1\) \(= 100\) .
Iepazīsti laukuma mēru pārveidojumus!
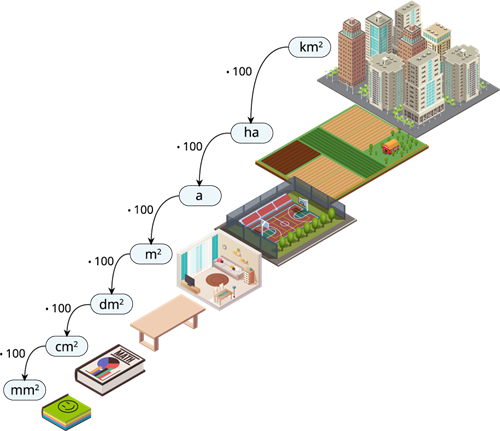
Lai noskaidrotu cik \(1\) ietilpst , \(1\) ir jāreizina ar \(100\), jeb \(1 · 100 = 100\) .
Tātad, \(1\) ietilpst \(100\) .
Tātad, pārveidojot no lielākas mēra vienības uz mazāku, reizina ar mērvienību skaitu!
Mazākā mērvienība ir daļa no lielās, tāpēc, ja vēlies pārveidot no mazākas uz lielāku laukuma mēra vienību, dali ar mērvienību skaitu!


Svarīgi!
Ievēro, ka laukuma mērvienībām ir pāra skaita nulles (divas, četras, sešas u.t.t.).
Nākamajos divos attēlos var redzēt, ka \(1\) \(ha\) ir mazāks nekā \(1\) .
\(1\) \(ha\) ir \(100\) reižu mazāks nekā \(1\) .

\(1\) \(ha\) \(=\) \(100\) \(· 100\) \(= 10000\)
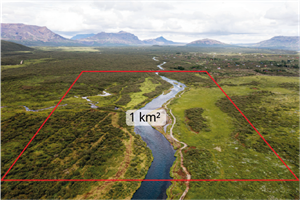
\(1\) \(= 1000\) \(· 1000\) \(= 1000000\)