Figūras laukums ir lielums, kas norāda, ar cik laukuma vienībām (tās savietojot) var noklāt figūru.
Tu jau proti noteikt figūras laukumu, izmantojot rūtiņu skaitu.
Taisnstūra laukumu Tu vari noteikt:
- izskaitot, cik rūtiņas noklāj šo taisnstūri;
- ar reizināšanas palīdzību - rūtiņu skaitu rindā reizinot ar rindu skaitu.
Atkārto to, izpildot uzdevumu!
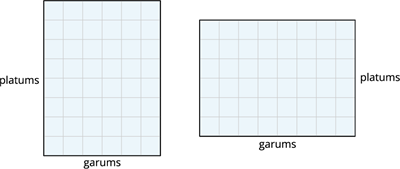
Attēlā pa kreisi, vienā rindā ir \(6\) rūtiņas un tādas ir \(8\) rindas. Laukums \(S\) \(= 6 · 8 = 48\) rūtiņas.
Attēlā pa labi, vienā rindā ir \(8\) rūtiņas un tādas ir \(6\) rindas. Laukums \(S\) \(= 8 · 6 = 48\) rūtiņas.
Taisnstūra laukuma skaitlisko vērtību iegūst, sareizinot blakus esošo malu garumu skaitliskās vērtības (izteiktas vienādās mērvienībās).
\(S\) \(=\) \(a\) \(·\) \(b\), kur \(a\) un \(b\) ir taisnstūra garums un platums.
\(S\) \(=\) \(a\) \(·\) \(b\), kur \(a\) un \(b\) ir taisnstūra garums un platums.
Attēlā pa kreisi, garums \(6\) \(cm\), platums \(8\) \(cm\). Laukums \(S\) \(= 6 · 8 = 48\) .
Attēlā pa labi, garums \(8\) \(cm\), platums \(6\) \(cm\). Laukums \(S\) \(= 8 · 6 = 48\) .
Svarīgi!
Nav svarīgi, kuru izmēru mēs uzskatām par garumu, kuru par platumu, galvenais izvēlēties blakus malu garumus. Reizinātājus mainot vietām reizinājums nemainās. Tātad taisnstūra laukums nemainās!
Taisnstūra malu garumi ir reizinātāji. Laukums ir reizinājums. Ir gadījumi, kad taisnstūra vienas malas garums nav zināms.
Svarīgi!
Iegūsti taisnstūra nezināmās malas garumu, dalot laukuma skaitlisko vērtību ar taisnstūra zināmās malas garumu!
Istabas grīdas garums ir \(6 m\) un tās laukums ir \(18\) .
Tad istabas platums ir \(18 : 6 = 3 m\)
Tad istabas platums ir \(18 : 6 = 3 m\)