Funkcija \(y = x^2\).
Uzzīmē funkcijas \(y = x^2\) grafiku, sastādot vērtību tabulu.
| -2,5 | -2 | -1 | 0 | 1 | 1,5 | 2 | 2,5 | 3 | |
| \(y\) | 6,25 | 4 | 1 | 0 | 1 | 2,25 | 4 | 6,25 | 9 |
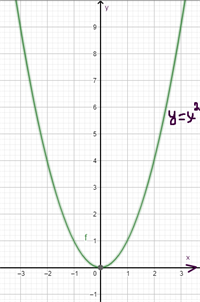
Savienojot atliktos punktus ar liektu līniju, iegūst funkcijas \(y = x^2\) grafiku.
Funkcija \(y = x^2\) ir pakāpes funkcija: lai noteiktu funkcijas vērtību kādā punktā, atbilstošā neatkarīgā mainīgā vērtība jākāpina kvadrātā.
Funkciju y = x² sauc par kvadrātfunkciju un tās grafiku par parabolu.
Grafiku var neierobežoti turpināt uz augšu.
Parabola y = \(x^2\) krusto \(x\) un \(y\) asis punktā \((0; 0)\) (grafiks iet caur koordinātu plaknes sākumpunktu.
Funkcija \(y = x^3\)
Funkcija \(y = x³\) ir pakāpes funkcija: lai noteiktu funkcijas vērtību kādā punktā, atbilstošais arguments jākāpina trešajā pakāpē - kubā.
Uzzīmē funkcijas \(y = x^2\) grafiku, sastādot vērtību tabulu.
| \(x\) | -2 | -1 | -0,5 | 0 | 1 | 1,5 | 2 |
| \(y\) | -8 | -1 | -0,125 | 0 | 1 | 3,375 | 8 |
Atliekot punktus koordinātu plaknē un savienojot tos ar liektu līniju, iegūst funkcijas \(y = x^3\) grafiku, kuru sauc pa kubisko parabolu.
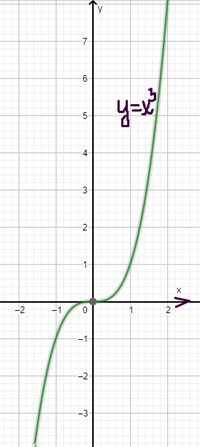
Funkciju y = x^3 sauc par trešās pakāpes funkciju.
Kubiskā parabola krusto \(x\) un \(y\) asis punktā \((0;0)\) ( grafiks iet caur koordinātu plaknes sākumpunktu)