Malu attiecība — teorija. Jaunās tēmas (izstrāde), Dz. Ozola.

Zīmējumā ir attēloti trīs taisnleņķa trijstūri. Zināms, ka \(EF || DK || AC.\)

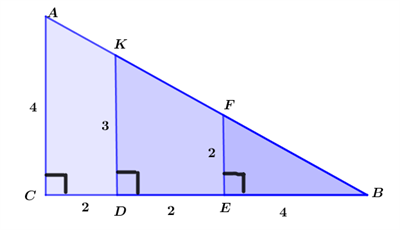
Visi trijstūri ir līdzīgi savā starpā, jo

∢ FEB = ∢ KDB = ∢ ACB = 90 °; ∢ B -

kopīgs.

Ja trijstūri ir līdzīgi, tad to attiecīgās malas ir proporcionālas.

\begin{array}{l} \frac{EF}{BE} = \frac{2}{4} = \frac{1}{2} \\ \frac{KD}{BD} = \frac{3}{6} = \frac{1}{2} \\ \frac{AC}{BC} = \frac{4}{8} = \frac{1}{2} \end{array}

Ja taisnleņķa trijstūriem leņķi ir vienādi, tad šajos trijstūros viena leņķa pretkatetes un piekatetes garumu attiecības ir vienādas.

Katešu garumu attiecības trijstūros ar vienādiem šauriem leņķiem ir vienādas.

Pretkatetes un hipotenūzas garumu attiecības trijstūros ar vienādiem šauriem leņķiem ir vienādas.

Piekatetes un hipotenūzas garumu attiecības trijstūros ar vienādiem šauriem leņķiem ir vienādas.

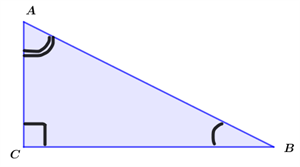
Leņķim \(A\):

\begin{array}{l} \frac{Pretkatete}{Piekatete} = \frac{BC}{AC} \\ \frac{Pretkatete}{Hipotenūza} = \frac{BC}{AB} \\ \frac{Piekatete}{Hipotenūza} = \frac{AC}{AB} \end{array}

Leņķim \(B\):

\begin{array}{l} \frac{Pretkatete}{Piekatete} = \frac{AC}{BC} \\ \frac{Pretkatete}{Hipotenūza} = \frac{AC}{AB} \\ \frac{Piekatete}{Hipotenūza} = \frac{BC}{AB} \end{array}

Piemērs:

Nosaki prasīto attiecību skaitliskās vērtības, ja dotais ir zīmējumā!

\begin{array}{l} \frac{AK}{AN} = \frac{6}{10} = \frac{3}{5} \\ \frac{AL}{AM} = \frac{9}{15} = \frac{3}{5} \\ \frac{AB}{AC} = \frac{12}{20} = \frac{3}{5} \end{array}

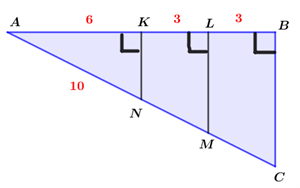
Piemērs:

Taisnleņķa trijstūrī \(ABC\) katešu attiecība ir \(3\) pret \(4\).

Nosaki leņķa B pretkatetes un hipotenūzas attiecību!

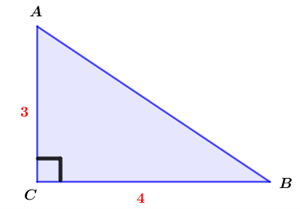
Lai aprēķinātu leņķa \(B\) pretkatetes attiecību pret hipotenūzu, vispirms ir jāaprēķina hipotenūzas garums.

\begin{array}{l} {AB}^{2} = {AC}^{2} + {BC}^{2} \\ {AB}^{2} = 3^{2} + 4^{2} \\ {AB}^{2} = 9 + 16 \\ {AB}^{2} = 25 \\ AB = 5 \end{array}

Uzraksta leņķa \(B\) pretkatetes un hipotenūzas attiecību

\frac{AC}{AB} = \frac{3}{5}

Atradi kļūdu?

1. Malu attiecība