OTRĀ SEMESTRA NOSLĒGUMA TESTI
Kas ir telpas plāns?
Plāns ir attēls, kas parāda telpas un tās objektu izvietojumu samazinātā izmērā. Tas noder, ja telpu nepieciešams plānot vai veikt tajā kādas izmaiņas, piemēram, būvniecību, remontu, mēbelēšanu. Vispirms iecerētās izmaiņas veic plāna un tikai tad - dabā.

Samazinājums šajā plānā ir \(1 : 100\)
|
Dabā
|
Plānā
|
|
\(1\) \(m \) \(=\) \(100\) \(cm\)
|
\(100\) \(cm\) \(:\) \(100\) \(=\) \(1\) \(cm\)
|
|
\(5\) \(m \) \(=\) \(500\) \(cm\)
|
\(500\) \(cm\) \(:\) \(100\) \(=\) \(5\) \(cm\)
|
|
\(10\) \(m \) \(=\) \(1000\) \(cm\)
|
\(1000\) \(cm\) \(:\) \(100\) \(=\) \(10\) \(cm\)
|
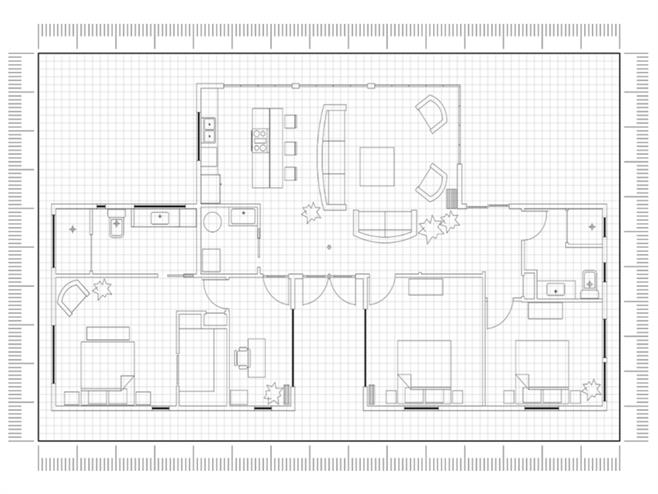
Dzīvokļa plāna piemērs
Evakuācijas plāna piemērs

Parka plāna piemērs

Kas ir telpas samazinājums plānā?
Telpas samazinājums jeb mērogs nosaka to, cik reižu visi attālumi dabā tiek samazināti plānā.
Piemērs:
Ja \(1\) \(m\) dabā atbilst \(1\) \(cm\) plānā, tad visi izmēri plānā ir samazināti \(100\) reižu.
Šādu samazinājumu pieraksta kā \(1 : 100\).
Dabaszinībās vari uzzināt vairāk par dažādu teritoriju attēlošanu plānā. Apskati to šeit!
Cik precīzi ir jāveic mērījumi veidojot plānu?
Piemēram, ja izmērītais garums ir , kā vajag rīkoties, lai to iezīmētu plānā?
Šādos gadījumos, lai atvieglotu mērījumus, izmanto noapaļošanu.
Atkarībā no uzdevumā prasītās precizitātes, mēra līdz tuvākajam pilnajam metram, decimetram vai centimetram.
Veikt mērījumus un atrast tuvāko pilno \(m\), \(dm\) vai \(cm\) var ar mērlentu.

Noapaļojot līdz veseliem metriem, jāatbild uz jautājumu, kuram no veseliem metriem norādītais skaitlis ir tuvāk?
Vai ir tuvāk \(7\) \(m\) vai \(8\) \(m\)?
Secinam, ka līdz \(7\) \(m\) atzīmei ir \(81\) \(cm\), bet līdz \(8\) \(m\) ir tikai \(19\) \(cm\).
Tātad noapaļojam uz veseliem \(8\) \(m\) ar uzviju un pierakstam šādi:
\(8\) \(m\).
Ja mērījums ir tieši pa vidu, piemēram, \(7\) \(m\) \(50\) \(cm\), tad to noapaļo ar uzviju uz \(8\) \(m\).
Noapaļojot līdz veseliem decimetriem (centimetru desmitiem), jāatbild uz jautājumu, kuram no decimetriem norādītais skaitlis ir tuvāk?
Vai ir tuvāk \(7\) \(m\) \(80\) \(cm\) vai \(7\) \(m\) \(90\) \(cm\)?
Šoreiz noapaļojam ar iztrūkumu uz \(7\) \(m\) \(80\) \(cm\) un pierakstam šādi:
\(7\) \(m\) \(80\) \(cm\).