OTRĀ SEMESTRA NOSLĒGUMA TESTI
Aplūkosim elektrisko ķēdi, kas sastāv no kondensatora, kvēlspuldzes un maiņsprieguma avota.
Izmantojot simulāciju, var pārliecināties, ka kvēlspuldze ķēdē ar kondensatoru kvēlo blāvāk, un plūstošais strāvas stiprums arī ir mazāks.
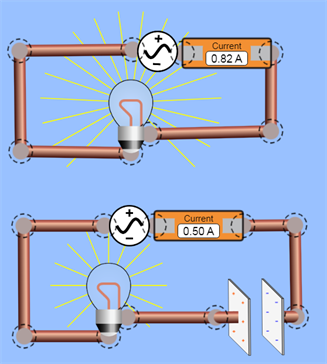
No tā izriet, ka kondensatoram maiņstrāvas ķēdē piemīt elektriskā pretestība, kuru sauc par kapacitīvo pretestību.
Kapacitīvā pretestība ir atkarīga no kondensatora kapacitātes.
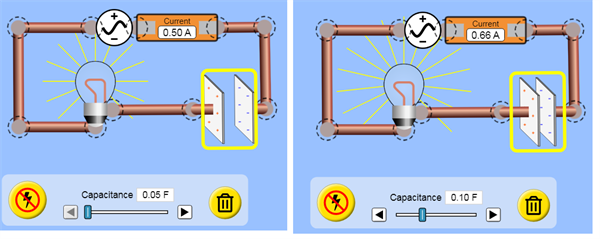
Palielinoties kondensatora kapacitātei, palielinās strāvas stiprums. No tā izriet, ka pretestība samazinās.
Secinājums: Kapacitīvā pretestība ir apgriezti proporcionāla kondensatora kapacitātei.
Kapacitīvā pretestība ir atkarīga no maiņstrāvas frekvences.
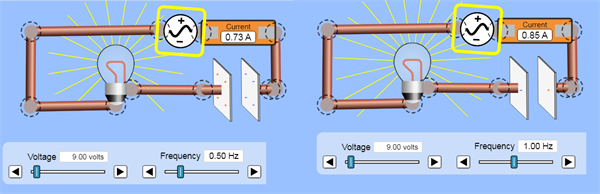
Palielinoties maiņstrāvas frekvencei, palielinās strāvas stiprums. No tā izriet, ka pretestība samazinās.
Secinājums: Kapacitīvā pretestība ir apgriezti proporcionāla maiņstrāvas frekvencei.
Kapacitīvo pretestību aprēķina pēc formulas:
, kur
— kapacitīvā pretestība,
— cikliskā frekvence, .
Aplūkosim elektrisko ķēdi, kas sastāv no kondensatora un maiņsprieguma avota.

Pieņemsim, ka ķēdei pieliktais spriegums laikā mainās pēc likuma , kur — sprieguma momentānā vērtība, — sprieguma maksimālā vērtība jeb amplitūda.
Lādiņš uz kondensatora klājumiem mainās pēc līdzīgā likumā, jo . Ķēdē plūstošo strāvas stiprumu noskaidro pēc formulas , kur — strāvas stipruma momentānā vērtība, — strāvas stipruma maksimālā vērtība jeb amplitūda.
No sakarībām un izriet, ka strāvas stipruma svārstības un sprieguma svārstības nesakrīt fāzē.

Taču sakarību var pārveidot par . Tātad strāvas stipruma svārstības apsteidz sprieguma svārstības par .
Izmantojot simulāciju, var pārliecināties, ka strāvas stipruma svārstības apsteidz sprieguma svārstības par .
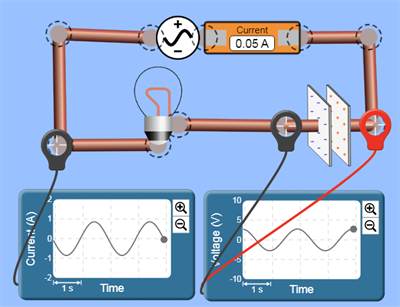
Vektordiagrammu zīmē šādi:
1. Izraugās strāvas asi .
2. No sākumpunkta \(O\) atliek strāvas stipruma maksimālo vērtību jeb amplitūdu ,
3. No sākumpunkta \(O\) atliek sprieguma maksimālo vērtību jeb amplitūdu , ievērojot, ka strāvas stipruma svārstības apsteidz sprieguma svārstības par jeb sprieguma svārstības atpaliek no strāvas stipruma svārstībām par .
