Skaitļu virkne līdz \(20\)
Noteiktā secībā sarakstītos skaitļus sauc par skaitļu virkni.
Skaitļu virkne parāda katru nākamo skaitli, tā palīdz atrisināt summu.
Ja zināsi skaitļa kaimiņus, vieglāk izdosies atrisināt darbības!
Skaitļu virkne līdz \(20\)
\(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(10\), \(11\), \(12\), \(13\), \(14\), \(15\), \(16\), \(17\), \(18\), \(19\), \(20\).
Pēc kārtas sakārtotu skaitļu virkni var redzēt arī uz skaitļu stara un uz lineāla.

Te būs jāieliek attēls ar skaitļu staru un lineālu
Skaitļu virkne ar pāra skaitļiem.
\(2\), \(4\), \(6\), \(8\), \(10\), \(12\), \(14\), \(16\), \(18\), \(20\).
Ieskaties, kā pāra skaitļus var atrast uz skaitļu stara!
Te attēls
Skaitļu virkne ar nepāra skaitļiem.
\(1\), \(3\), \(5\), \(7\), \(9\), \(11\), \(13\), \(15\), \(17\), \(19\).
Ieskaties, kā pāra skaitļus var atrast uz skaitļu stara!
Te attēls
Kā saskaitā skaitļus \(20\) apjomā bez pārejas citā desmitā?
Divu un vairāku skaitļu saskaitīšanu sauc par summu.
Atceries, kā sauc darbības locekļus saskaitīšanas darbībā!

Tev būs vieglāk apgūt saskaitīšanu \(20\) apjomā, ja atkārtosi jau iepriekš apgūto:
- atkārto skaitļa sastāvu pirmajā desmitā šeit!
- atkārto, kā var saskaitīt \(10\) apjomā bez pārejas citā desmitā šeit!
Vēro attēlā, kā vari saskaitīt \(20\) apjomā bez pārejas citā desmitā!
Pievērs uzmanību! Pirmā darbība tiek risināta pirmajā desmitā, otrā darbība tiek veikta otrajā desmitā.
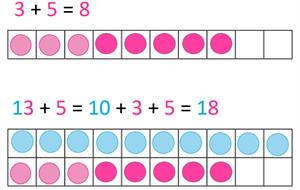

Ja pirmajā desmitā proti atrisināt summu, tātad arī otrajā desmitā tas izdosies!
No sākuma saskaiti vienus savā starpā un tad pieskaiti pie desmit.
\(3\) \(+\) \(5\) \(=\) \(8\)
\(13\) \(+\) \(5\) \(=\) \(18\)
Vēro, kā šo pašu darbību varam parādīt uz skaitļu stara!
\(13 + 5 = 10 + 3 + 5 = 18\)

Vienādu skaitļu saskaitīšana jeb dubultošana
\(1\) \(+\) \(1\) \(=\) \(2\)