Zinot to, ka daļas saucējs norāda, cik daļās veselais ir sadalīts, bet skaitītājs - cik daļas ir paņemtas, var noteikt, kura daļa ir lielāka, kura - mazāka, vai arī varbūt tās ir vienādas.
Tātad - daļas var salīdzināt.
Aplūko piemēru: Mamma uzcepa picu un sadalīja to \(6\) vienādās daļās. Māsa apēda \(2\) gabalus no picas, bet brālis - \(3\) gabalus. Kurš no viņiem apēda vairāk picas?
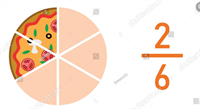 vai
vai 
Attēlā skaidri redzams, ka brālis, kurš apēda picas, apēda vairāk nekā māsa, kura apēda picas.
Ja daļām ir vienādi saucēji, tad lielāka ir tā daļa, kurai skaitītājs ir lielāks.
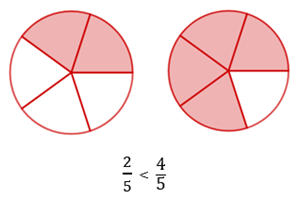
Attēlā redzams, ka figūra ir sadalīta \(5\) daļās. Vienā gadījumā iekrāsotas ir \(4\) daļas, otrā gadījumā - \(2\) daļas. Tāpat uzskatāmi redzams, ka \(4\) daļas ir lielāka figūras daļa, nekā \(2\) daļas, tātad \(>\)
Daļas var salīdzināt arī uz skaitļu stara. Tas izskatās šādi:
