Taisnstūra paralēlskaldni no visām pusēm ierobežo taisnstūri!
Taisnstūris ir četrstūris, kuram visi leņķi ir taisni un pretējās malas ir vienāda garuma.
Taisnstūra paralēlskaldņa paralēlās šķautnes ir taisnstūra paralēlskaldņa sānu skaldņu jeb taisnstūra pretējās malas!
Matemātikā izmanto simbolu \(||\), lai pierakstītu paralēlās malas!
piem. \(EF\) \(||\) \(GH\), jo ir taisnstūra \(EFGH\) pretējās malas
\(EF\) \(||\) \(AB\), jo ir taisnstūra \(AEFB\) pretējās malas
\(AB\) \(||\) \(DC\), jo ir taisnstūra \(ABCD\) pretējās malas
\(DC\) \(||\) \(HG\), jo ir taisnstūra \(DHGC\) pretējās malas
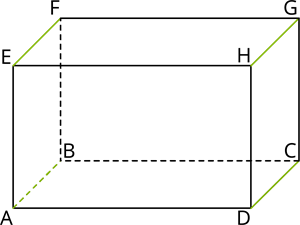
Ja jāizvēlas dotajai šķautnei paralēlās šķautnes, tad mēs izvēlamies tās šķautnes, kas atrodas vienā plaknē ar doto šķautni.
Šķautnei \(AB\) paralēlās šķautnes ir \(EF\) un \(DC\), jo \(AB\) ir kopīgā šķautne gan skaldnei \(AEFB\), gan skaldnei \(ABCD\).
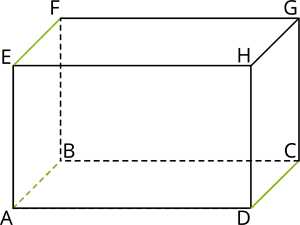
Taisnstūra paralēlskaldņa perpendikulārās šķautnes ir taisnstūra paralēlskaldņa skaldņu jeb taisnstūra perpendikulārās malas.
Svarīgi!
Taisnstūra visi leņķi ir taisni! Tas nozīme, ka malas, kas veido taisno leņķi ir perpendikulāras!
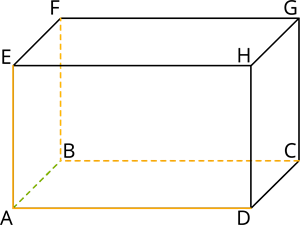
Dotajā attēlā šķautnei \(AB\) perpendikulāra šķautne ir
\(AD\), jo kopā ar malu \(AB\) veido taisnstūra \(ABCD\) taisno leņķi \(A\);
\(BC\), jo kopā ar malu \(AB\) veido taisnstūra \(ABCD\) taisno leņķi \(B\);
\(AE\), jo kopā ar malu \(AB\) veido taisnstūra \(AEFB\) taisno leņķi \(A\);
\(BF\), jo kopā ar malu \(AB\) veido taisnstūra \(AEFB\) taisno leņķi \(B\)!