Atkārtojums. cos x=a atrisināšana no vienības riņķa — teorija. Matemātika (Skola2030), Matemātika II.

Vienādojumu

\cos x = a

ērti atrisināt, izmantojot vienības riņķa līniju. Trigonometriskais vienības riņķis ir dots matemātika I eksāmena formulu lapā.

Atrisināsim vienādojumu

\cos x = \frac{\sqrt{2}}{2}

Uz kosinuss ass atliksim vērtību

\frac{\sqrt{2}}{2}

. Ir divi pagrieziena leņķi, kuru kosinuss ir

\frac{\sqrt{2}}{2}

. Virs $x$ ass un zem $x$ ass.

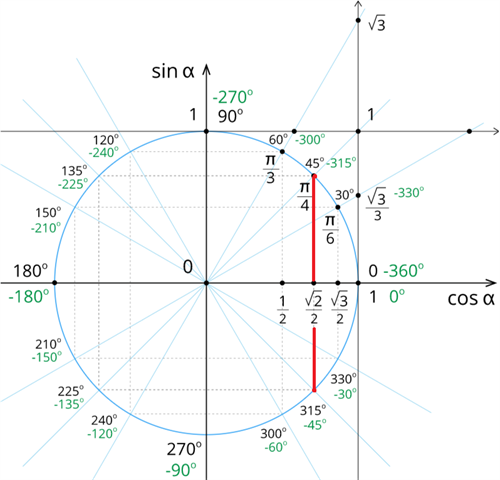
Dotajai vērtībai atbilst leņķi

45 °

- 45 °

Tā kā pieskaitot vai atņemot vienu vai vairākas reizes pilnu leņķi

2 π

, atkal iegūst pagrieziena leņķi, kura kosinuss ir

\frac{\sqrt{2}}{2}

, tad vienādojumam ir bezgalīgi daudz atrisinājumu.

Vienādojuma

\cos x = \frac{\sqrt{2}}{2}

atrisinājums ir

Ja izsaka ar grādiem:

x = [\begin{array}{l} 45 ° + 360 ° n \\ - 45 ° + 360 ° n, n \in ℤ \end{array}

Ja izsaka ar radiāniem:

x = [\begin{array}{l} \frac{π}{4} + 2 π n \\ - \frac{π}{4} + 2 π n, n \in ℤ \end{array}

Šīs atbildes var apvienot vienā:

x = \pm 45 ° + 360 n, n \in ℤ

jeb

x = \pm \frac{π}{4} + 2 π n, n \in ℤ

Piemērs:

Atrisini vienādojumu

\cos x = - \frac{1}{2}

x = \pm 120 ° + 360 ° n, n \in ℤ

, ja atbildi pieraksta ar grādiem.

x = \pm \frac{2 π}{3} + 2 π n, n \in ℤ

, ja atbildi pieraksta ar radiāniem

Ja vien tas nav prasīts, abos veidos atbildi nav jāraksta.

Iegaumē atrisinājums šādiem vienādojumiem (visur atrisinājumos $n \in ℤ$ ):

$\cos x = 1$ . Atrisinājums ir $x = 2 π n$ jeb $x = 360 ° n$ .
$\cos x = 0$ . Atrisinājums ir $x = \frac{π}{2} + π n$ jeb $x = 90 ° + 180 ° n$ .
$\cos x = - 1$ . Atrisinājums ir $x = π + 2 π n$ jeb $x = 180 ° + 360 ° n$ .

Atceries!

Vienādojumam

\cos x = a

eksistē atrisinājums, ja

- 1 \leq a \leq 1

jeb

|a| \leq 1

Atradi kļūdu?

5. Atkārtojums. cos x=a atrisināšana no vienības riņķa