Koka diagramma ir viens no veidiem, kā var parādīt un sistematizēt visus savienojumus. Ar koka diagrammu tiek veikta pilnā pārlase.
Piemērs:
Cik dažādus divciparu skaitļus var izveidot no cipariem 1, 2 un 3, ja katru izmanto tieši vienu reizi.
Risinājums:
Izveido koka diagrammu:
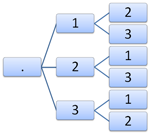 |
\(= 12\)
\(= 13\)
\(= 21\)
\(= 23\)
\(= 31\)
\(= 32\)
|
Atbilde: var iegūt 6 dažādus skaitļus.
Aplūkosim 3. piemēru:
Cik dažādos veidos var izveidot dežurantu pāri, ja klasē ir palikuši 4 skolēni: Aija, Vita, Reinis un Juris?
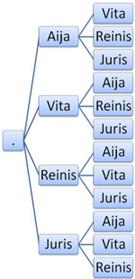 |
1. Aija un Vita
2. Aija un Reinis
3. Aija un Juris
4. Vita un Aija
5. Vita un Reinis
6. Vita un Juris
7. Reinis un Aija
8. Reinis un Vita
9. Reinis un Juris
10. Juris un Aija
11. Juris un Vita
12. Juris un Reinis
|
No koka diagrammas redzam, ka ir tikai 6 dežurantu pāri - Aija un Vita; Aija un Reinis; Aija un Juris; Vita un Reinis; Reinis un Juris; Vita un Juris, jo katrs pāris atkārtojas divas reizes.
Atrisināsim 4. piemēru:
Cik dažādos veidos var izvēlēties divus skolēnus, pirmo - par tāfeles tīrītāju, otro - par grīdas slaucītāju, ja klasē ir palikuši: Aija, Vita, Reinis un Juris?
Izmanto to pašu koka diagrammu, bet šajā gadījumā atbilde būs 12, jo katrs no koka diagrammā uzrādītajiem pāriem ir atšķirīgs. Ja skolēnus maina vietām, mainās to lomas.
Ar koka diagrammu ieguvām dažādus rezultātus, jo 3. un 4. piemērā tika aplūkoti divi atšķirīgi savienojumu veidi: kombinācijas un variācijas.
Svarīgi!
Ievēro: kombinatorikas uzdevumos parasti par savienojumiem atbild uz jautājumu: cik nevis - kādi
Tabula
Atsevišķos gadījumos, lai sistematizētu datus, ir izdevīgi veidot savienojumu tabulu.
Piemērs:
Metamo kauliņu met divas reizes un punktus sareizina. Cik dažādus reizinājumus ir iespējams iegūt?
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
|
2
|
2
|
4
|
6
|
8
|
10
|
12
|
|
3
|
3
|
6
|
9
|
12
|
15
|
18
|
|
4
|
4
|
8
|
12
|
16
|
20
|
24
|
|
5
|
5
|
10
|
15
|
20
|
25
|
30
|
|
6
|
6
|
12
|
18
|
24
|
30
|
36
|
Dažādie reizinājumi ir 1; 2; 3; 4; 5; 6; 8; 9; 10; 12; 15; 16; 18; 20; 24; 25; 30; 36 - kopā 18 dažādi rezultāti.