Pirms sāc lasīt par viļņu veidiem, obligāti atkārto iepriekšējo materiālu:
Pastāv dažādas viļņu klasifikācijas.
Piemēram, pēc viļņu dabas izšķir šādus viļņus: mehāniskie viļņi, elektromagnētiskie viļņi, de Brojī viļņi un gravitācijas viļņi.

Mehāniskais vilnis
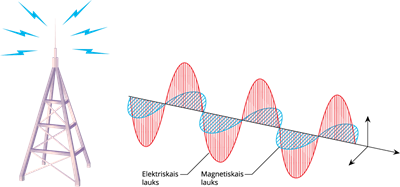
Elektromagnētiskais vilnis
Viļņi atšķiras arī pēc viļņu frontes veida. Piemēram, pastāv plakanie viļņi, kuriem viļņu fronte ir plakne. Savukārt sfēriskiem viļņiem viļņu fronte ir sfēra.
 |
 |
 |
|
plakans vilnis
|
sfēriskais vilnis
|
cilindriskais vilnis
|
Pēc iespējamajiem izplatīšanās virzieniem izšķir šādus viļņus: viendimensionālie viļņi, kas izplatās tikai vienā noteiktā virzienā; divdimensionālie viļņi, kas izplatās dažādos virzienos pa noteiktu virsmu, un trīsdimensionālie viļņi, kas izplatās visos telpas virzienos.
Viļņus var klasificēt pēc svārstību virziena attiecībā pret viļņu izplatīšanās virzienu. Izšķir šķērsviļņus (svārstības notiek perpendikulāri viļņu izplatīšanās virzienam) un garenviļņus (svārstības notiek viļņu izplatīšanās virzienā).
 |
 |
|
garenvilnis
|
šķērsvilnis
|
Pēc enerģijas pārneses izšķir šādus viļņus: skrejviļņi (pārnes enerģiju, bet nepārnes vielu) un stāvviļņi (nepārnes gan vielu, gan enerģiju).
 |
 |
|
skrejvilnis
|
stāvvilnis
|
Stāvvilnim katrā vietā ir sava raksturīga svārstību amplitūda. Punktus, kuros nenotiek kustība, sauc mezglu punktiem jeb mezgliem. Savukārt punktus, kuros svārstības notiek ar maksimālo amplitūdu, sauc par blīzuma punktiem (blīzumiem). Zīmējumā mezgli ir nodalīti ar sarkano, bet blīzumi atrodas viduspunktā starp jebkuriem diviem blakus esošiem mezgliem.
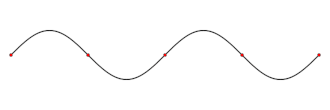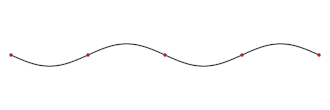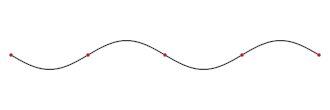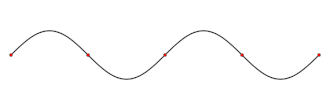
Attālums starp diviem blakus esošiem mezgliem (vai blīzumiem) ir vienāds ar viļņa garuma pusi. Tātad attālums starp blakus esošo mezglu un blīzumu ir viļņa garuma ceturtdaļa.
Stāvvilnis veidojas, ja vilnis savā ceļā sastop šķērsli un atstarojas no tā pretējā virzienā. Piemēram, mūzikas instrumentu spēlēšana pamatojas uz to, ka tajos veidojas stāvviļņi. Stāvviļņi veidojas stīgu instrumentos un pūšamajos instrumentos.
Stāvvilnis veidojas, ja vilnis savā ceļā sastop šķērsli un atstarojas no tā pretējā virzienā. Piemēram, mūzikas instrumentu spēlēšana pamatojas uz to, ka tajos veidojas stāvviļņi. Stāvviļņi veidojas stīgu instrumentos un pūšamajos instrumentos.
Aplūkosim stāvviļņu veidošanos stīgā ar garumu \(L\).
 |
 |
 |
|
Stīgas pamattoņa svārstības
|
Stīgas pirmā virstoņa svārstības
|
Stīgas otrā virstoņa svārstības
|
| Stīga ir nostiprināta abos galos. No tā izriet, ka tai ir vismaz divi mezglu punkti. Zīmējumā var redzēt, ka visā stīgas garumā ietilpst viens pusviļņa garums. Tātad stīgas stāvviļņa garums . | Ja stīgā novietojas trīs mezglu punkti, tad stīga ietilpst divus pusviļņa garumus. Šādas svārstības sauc par pirmā virstoņa svārstībām. |
Ja stīgā novietojas četri mezglu punkti, tad stīga ietilpst trīs pusviļņa garumus. Šādas svārstības sauc par otrā virstoņa svārstībām.
|
Stāvviļņu rašanos var novērot caurulē ar gaisu. Frekvenču ģeneratoru izmanto kā viļņu avotu, ber skaņas sensoru — stāvviļnu reģistrācijai.
Aplūkosim cauruli ar atvērtiem galiem.
 |
 |
 |
|
Pamattoņa svārstības
|
Pirmā virstoņa svārstības
|
Otrā virstoņa svārstības
|
|
Caurules gali ir atvērti. No tā izriet, ka ir vismaz divi blīzumu punkti. Tātad starp tiem atrodas viens mezglu punkts.
Ievērojot, ka attālums starp diviem blakus esošiem blīzumiem ir vienāds ar viļņa garuma pusi, var secināt ka stāvviļņa garums
|
Ja caurulē novietojas trīs blīzumu punkti, tad starp tiem būs divi mezglu punkti. Šādas svārstības sauc par pirmā virstoņa svārstībām.
|
Ja caurulē novietojas četri blīzumu punkti, tad starp tiem būs trīs mezglu punkti. Šādas svārstības sauc par pirmā virstoņa svārstībām.
|
Lai aprēķinātu citu virstoņu viļņu garumus, var izmantot formulu:
Aplūkosim cauruli ar vienu atvērto galu.
 |
 |
 |
|
Pamattoņa svārstības
|
Pirmā virstoņa svārstības
|
Otrā virstoņa svārstības
|
| Viens caurules gals ir atvērts. No tā izriet, ka ir vismaz viens blīzuma punkts. Otrais gals ir aizvērts. Tātad ir vismaz viens mezglu punkts. Attālums starp blakus esošo mezglu un blīzumu ir viļņa garuma ceturtdaļa. Tātad . | Ja blīzumu un mezglu skaits palielinās par vienu, tad caurulē veidosies divi blīzumu punkti un divu mezglu punkti. Tātad pirmā virstoņa viļņa | Ja caurulē veidojas trīs blīzumu punkti un trīs mezglu punkti, otrā virstoņa viļņa garums ir vienāds ar |
Lai aprēķinātu citu virstoņu viļņu garumus, var izmantot formulu: