1. Svārstu enerģijas

Pirms sākt šo tēmu, obligāti atkārto iepriekšējo gadu tēmas:

 

Enerģija raksturo ķermeņa spēju veikt darbu. Enerģiju mēra džoulos (\(J\)).

Kinētiskā enerģija piemīt visiem kustībā esošiem ķermeņiem. Tā ir vienāda ar pusi no masas un ātruma kvadrāta reizinājuma $E_k=\frac{m{v}^2}{2}$.

Potenciālā enerģija piemīt gan virs zemes paceltiem ķermeņiem (piemēram, akmens krītot no paaugstinājuma, zemē izveido iedobi), gan elastīgi deformētiem ķermeņiem (piemēram, uzvilkts loks izšauj bultu). Gravitācijas potenciālo enerģiju aprēķina pēc formulas $E_p=\mathit{mgh}$, savukārt elastības potenciālo enerģiju — $E_p=\frac{k{x}^2}{2}$, kur \(m\) — ķermeņa masa, \(h\) — augstums, \(v\) — ātrums, \(k\) — elastības koeficients, \(x\) — absolūtais pagarinājums.

 

Norisinoties svārstībām, nepārtraukti notiek uzkrātās gravitācijas potenciālās enerģijas pāriešanā kinētiskajā enerģijā un pēc tam pretēji — kinētiskā enerģija atkal pāriet gravitācijas potenciālajā enerģijā.

Aplūkosim diega svārsta svārstības.

 

 

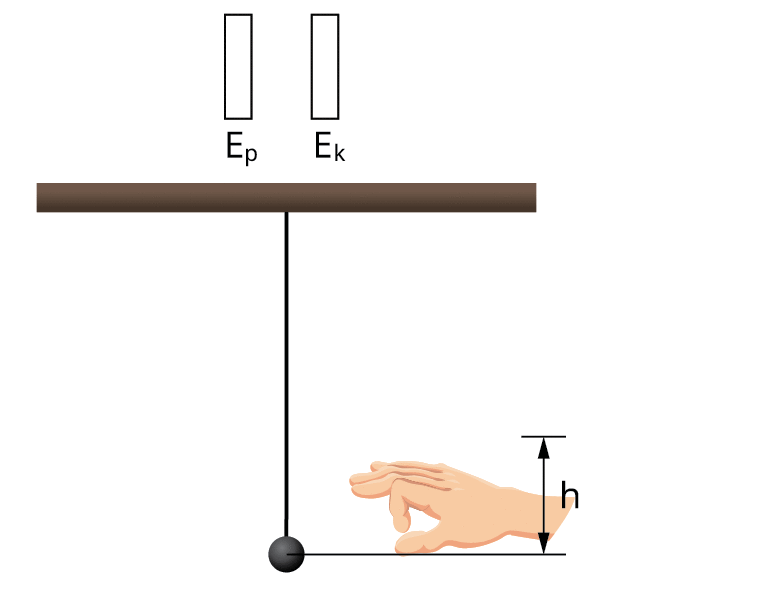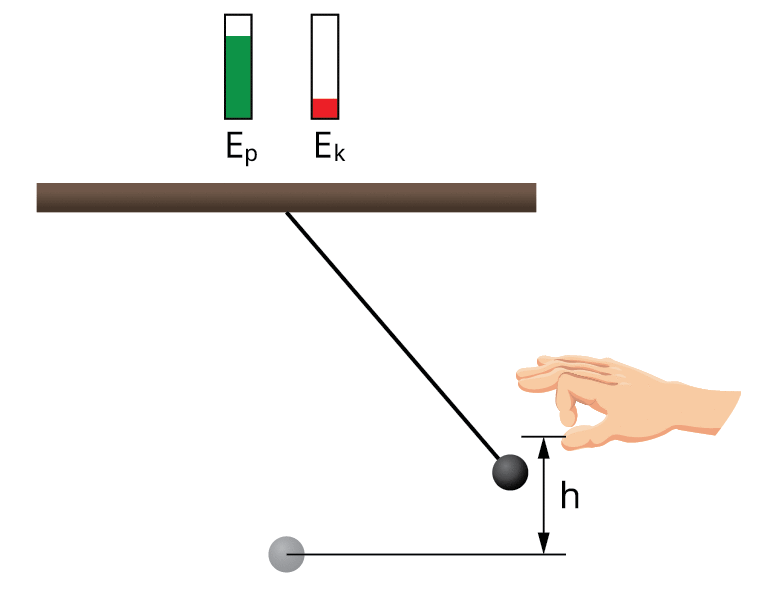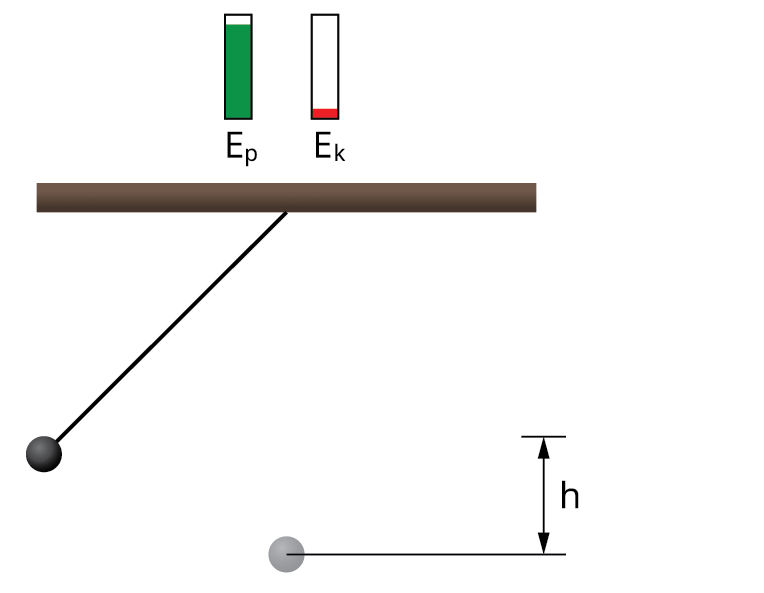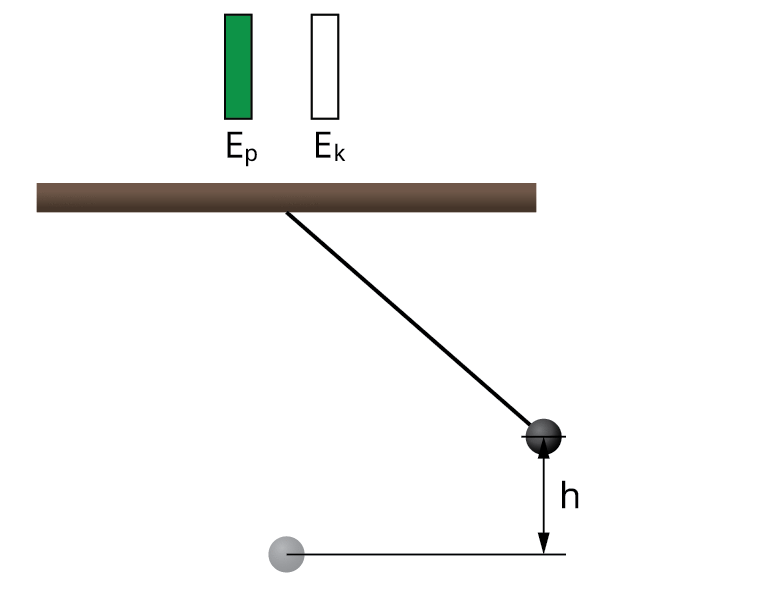
Viena svārstību perioda laikā abu enerģiju apmaiņa notiek divas reizes. Tā tas turpinātos neierobežotu laiku, ja vien svārstības būtu nerimstošas, proti, nepastāvētu berze un pretestības spēks. Nerimstošu svārstību gadījumā svārstību sistēmas pilnā mehāniskā enerģija ir kinētiskās un potenciālās enerģijas summa un tā visu laiku paliek nemainīga.
Tā svārstībām izpaužas enerģijas nezūdamības likums $E=E_k+E_p=\mathit{const}$, kur
$E$ — sistēmas kopējā enerģija jeb pilnā, \(J\)
$E_k$ — kinētiskā enerģija, \(J\)
$E_p$ — potenciālā enerģija, \(J\)

Aplūkosim diega svārsta koordinātas grafiku.

 

Eksperimenta sākumā (lodīte atrodas zīmējuma labajā pusē) $E_k$ = \(0\), bet $E_p=\mathit{mgh}$. Tas atspoguļots enerģiju grafikos.

 

Lodītei, sasniedzot viszemāko pozīciju, $E_p$ = \(0\), bet $E_k=\frac{m{v}^2}{2}$.

 

Kad lodīte sasniedz augstumu h zīmējuma kreisajā pusē, tad $E_k$ = \(0\), bet $E_p=\mathit{mgh}$.

Grafikos ir redzams, ka enerģijas svārstību frekvence ir divas reizes lielāka nekā koordinātas svārstību frekvence.

Līdzīga situācija notiek arī ar atsperes svārstu, kas svārstās horizontālajā plaknē.

 

 

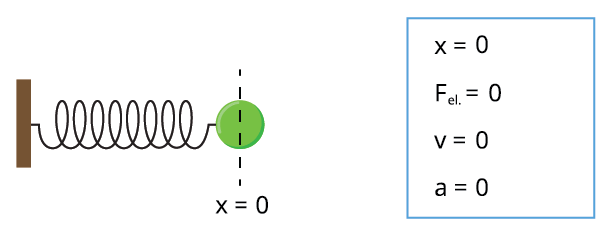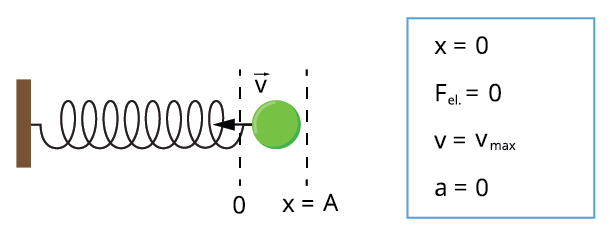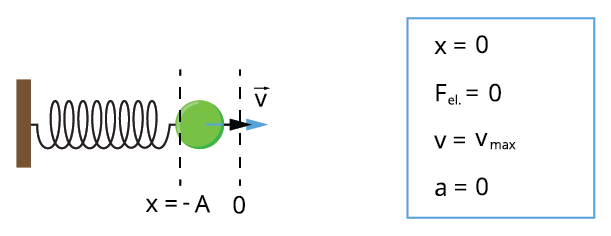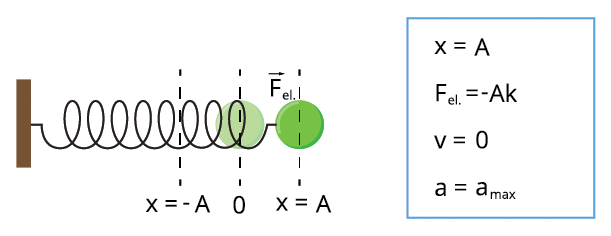
Pieņemsim, ka eksperimenta sākumā (lodīte atrodas zīmējuma labajā pusē). $E_k$ = \(0\), bet potenciālā enerģija — $E_p=\frac{k{x}^2}{2}$. Lodītei, sasniedzot pozīciju \(0\), $E_p$ = \(0\), bet $E_k=\frac{m{v}^2}{2}$. Kad lodīte atrodas zīmējuma kreisajā pusē, tad $E_k$ = \(0\), bet $E_p=\frac{k{x}^2}{2}$. Enerģijas svārstību frekvence ir divas reizes lielāka nekā koordinātas svārstību frekvence.

Kad atsperes svārsts svārstās vertikālajā plaknē, jāievēro gan kinētiskās, gan gravitācijas un elastības potenciālās enerģijas izmaiņas.

 

 

Piemēram, uzsākot svārstības no apakšas, svārstību sistēmas enerģija ir vienāda:

 

$E_p=\frac{k{x}^2}{2}$.

Savukārt, līdzsvara stāvoklī svārstību sistēmas enerģija ir vienāda ar:

 

$E_k=\frac{m{v}^2}{2}$ un $E_p=\mathit{mgh}$ summu. Lodītei atrodoties visaugstākajā pozīcijā, svārstību sistēmas enerģiju veido gan gravitācijas potenciālā enerģija $E_p=\mathit{mg}\cdot 2h$, gan elastības potenciālā enerģija:

 

$E_p=\frac{k{x}^2}{2}$.